粒子径基準の例)個数、長さ、面積、体積、質量など 縦軸の例)Q:積算分率、q:頻度 粒子径: JISではxを粒子径又は球形粒子の直径を表現する記号として 使用します。また、dも広く使用されています。 直径 JIS Z 191 1999参照 測定値及び測定基準 粒子径x体積と表面積の違い類似用語の違いを比較する 面積は、というと、6つの面があるのですから、「6平方センチメートル」です。 単位がついていると面倒なので、単位を除くと、 体積1 : 表面積6 ということですね。立方体 直方体 断面積から体積計算 公式 求め方 高さ 底面積 自動 volume

角柱 円柱の表面積と体積の公式 数学fun
面積と体積の違い
面積と体積の違い-人間の体で言ったら 皮膚とか空気に触れる部分なんかが表面積 体積は人間そのものの大きさ 円柱とかだったら、表面積は展開図の面積全部。 体積は組み立てたときの三次元って感じの大きさ だから、円柱とかなら体積は底面積と高さをかけるわけなのよ47 7 立体の体積と表面積 133 次の図の直方体の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 137 次の図の立体の体積と表面積を求めよ。 ⑴ ⑵ 135 次の図の円柱の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 134 右 の図は ,円柱とその展開図である。 次の問いに答えよ。




これで分かる 面積と体積の違い コーチング1グループ発達障害ブログ
立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V (x) で表し, x における断面積を S (x) とおきます. が示されます. (底辺)×(高さ h ) になる. 同様にし面積と2重積分から体積と3重積分へ 面積を計算する時 に、千 切りばか が能ではあ ませ ん。みじ したって良い 筈です。つまり、領域D を縦dy、横dxの(各辺が座標軸に平行な)微小長方形に分割 し、1枚の面積dxdy を領域D 内で全部足せば全体の面積に 面積効果による色の見え方の違い 面積の大小によって色の見え方が変わるのは理解できたものの「具体的にどのような色の変化が起きるの?」という疑問が出てきます。 ここでは面積効果による色の見え方の違いを解説します。 明るい色
※ 球の表面積は円の面積の4倍になる.(非常にきれいな関係) ※ 高校数学IIIで微分を習えば,体積 V= πr 3 を半径で微分すると表面積 S=4πr 2 になることが分かる.脱線ついでに言えば,円の面積 S=πr 2 を半径で微分すると円周の長さ L=2πr になる.1・2・4等価単位体積重量 可動部の重量をその 体積で除した値をいろ 1・2・5基 準状態 温度0℃,気 圧760mmHgの 状態をいろ 1・3測 定原理 流体の鉛直管路内に自由に上下する可動部をもろ け,そ のフロートまたはピストンが,流 通面積を増減×体積8 : 表面積48 ではなく、 体積8 : 表面積24 という比です。 この関係は、仮に体積を100倍にしても1000倍にしても同じ傾向になります。気が向いたら頭の中でためしてみて下さい。
体積と重量の違いは?1分でわかる重量の計算、比重との違い、鉄の重量換算 100円から読める!ネット不要!印刷しても読みやすいpdf記事はこちら⇒ いつでもどこでも読める!広告無し!建築学生が学ぶ構造力学のpdf版の学習記事 容積と体積の違いは面積や体積など,客観的にだれが判断しても「大きい」ものに対して使います。 数量を表すとき(numberやamountなど)は large を使います。big は使いません。 big 面積や体積などに限らず,主観的にその人の判断で決められる「大きい」ものに対しても使い 体積やかさは、なかなかに難しい単元です。 面積や長さはまだ紙の上には書くことができても、立体となるとそうもいきません。 体積やかさに関する記事を集めました。 かさ・体積・容積のまとめ 小学2年生に体積・かさの単位変換をマ



円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典



円錐とは 体積 表面積の公式や求め方 受験辞典
側面積と表面積と体積の計算の違いがわかりません Clear M2 平米 とm3 立米 は換算 変換 方法 計算問題を解いてみようでも、立方体って直方体の体積と同じように (たて)×(よこ)×(高さ) これじゃダメなのかな? そんな疑問を抱く人もいるでしょう。 というわけで次は立方体と直方体の違いについてみておきましょう。 立方体と直方体って何が違う?比表面積・細孔分布 粒子径測定における個数分布と質量(体積)分布との違いとは? (体積)分布とはふるいで粒子の大きさを測定した際のイメージです。つまり粒子の大きさを質量の分布として表記




体積 表面積




立体の体積について 小5 小6 中1 中2 中3 家庭教師とっしゅ先生の授業 小学生 中学生
体積と面積の違いは? 面積が2次元、体積が3次元 1 1年以上前 ?? 0 この回答にコメントする NIkumann 1年以上前 面積は、平面 体積は、立体 です。 今回は三角柱、三角錐、円柱、円錐・・など様々な図形の体積と表面積の求め方についての記事をまとめました。 図形ごとに求め方が違い、1つ1つ覚えていくのは大変です。 しかし、 図形問題や円周率の問題はセンター試験でも多く出題されます。 これ 違いは、 面積はサイコロで例えると一面の大きさ。 体積はサイコロ全体の大きさ。 面積は平面。平ら。 体積は立体。 似ているところは、 公式に『縦×横』が入ること。 広さを指す言葉であること。 単位にmが付くこと。 考えてみたけど間違っていたら




体積の求め方 計算公式一覧




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう! 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱の体積を求めなさい。ただし 面積と体積は、具体的にどのような違いがあるんですか? 面積と体積は、具体的にどのような違いがあるんですか? 面積は表面的な大きさを表していて、体積というのはコップなどのように液体でも気体でも何かがどれだけはいるかをあらわしています。面積は、たとえば であれば、縦×横の 底面積が3m2の立方体の高さは2mです。このときの立方体の体積はいくらになるでしょうか。 解答 上の定義に従って計算を行っていきましょう。 3 × 2 = 6m3と求めることができました。
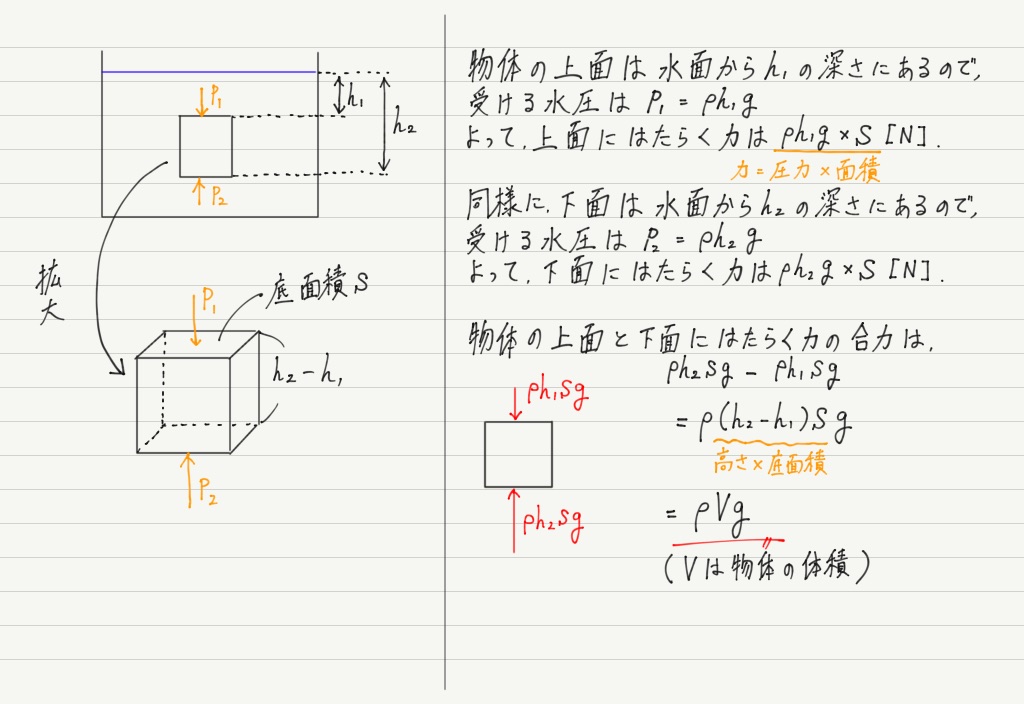



圧力 水圧 浮力 高校物理をあきらめる前に 高校物理をあきらめる前に
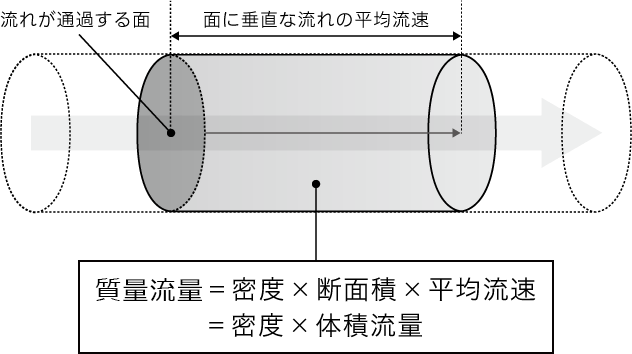



体積流量と質量流量 流量の基本を知る 流量知識 Com キーエンス
体積、容積とかさの違い 三角形の面積はなぜ底辺×高さ÷2なの?鋭角三角形、直角三角形、鈍角三角形のそれぞれについて解説します! 円周や円の面積を求めるときに使う円周2角柱と円柱 角柱・円柱の体積=底面積×高さ 角柱・円柱の表面積=底面積×2側面積 3角すいと円すい比表面積は単位重量の粉体中に含まれる全粒子の表 面積の総和Sw(cm2/g) であらわすのが普通であるが, 単位体積あたりの全表面積Sv(cm2/cm3) で示すこと もある ここで単位体積というのは粉体の見かけ体積 (かさ) ではなく固体分だけの実質体積である した




6 2 図形を1回転させた時の体積比 側面積比 表面積比を求めるには さんすうがく パート 2




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
体積・容量の換算 V olume conversion (1) 1m3 =103l =104dl =105cl =106ml (2) 1acreft = ft3, 1ft3= 1,728in3 (3) 1gal = 4quart =8pint =32gil (4) I mperial 1barrel =36gal, 1gil =5fluid ouns (5) US fluid 1barrel =315gal, 1gil =4fluid ouns (6) US dry 1barrel =2625gal (7) P etroleum 1barrel = 42gal(US fl) (8) J apanese 1koku
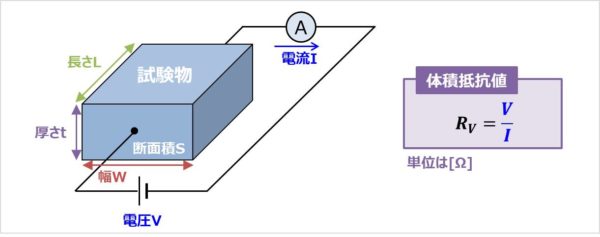



体積抵抗率 と 体積抵抗値 の違い 単位や測定方法について Electrical Information




筋体積から考える 効率的なトレーニングとは Karadabase




蓄熱web講座 Pro 解説コラム



面積 表面積 体積の違いってなんですか 表面積は見えているところだけで例えば白 Yahoo 知恵袋



底面積 側面積 表面積 回転体 中学1年数学 空間図形
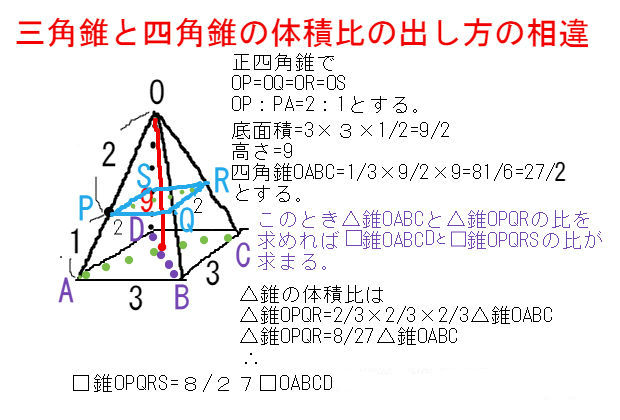



三角錐と四角錐の体積比計算方法の違い 中学数学 理科 寺子屋塾の復習サイト




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




角柱 円柱の表面積と体積の公式 数学fun



体積と面積の違いは 1分でわかる違い 意味 公式と求め方




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学




これで分かる 面積と体積の違い コーチング1グループ発達障害ブログ




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書




長さ面積体積の単位まとめ 家庭学習レシピ
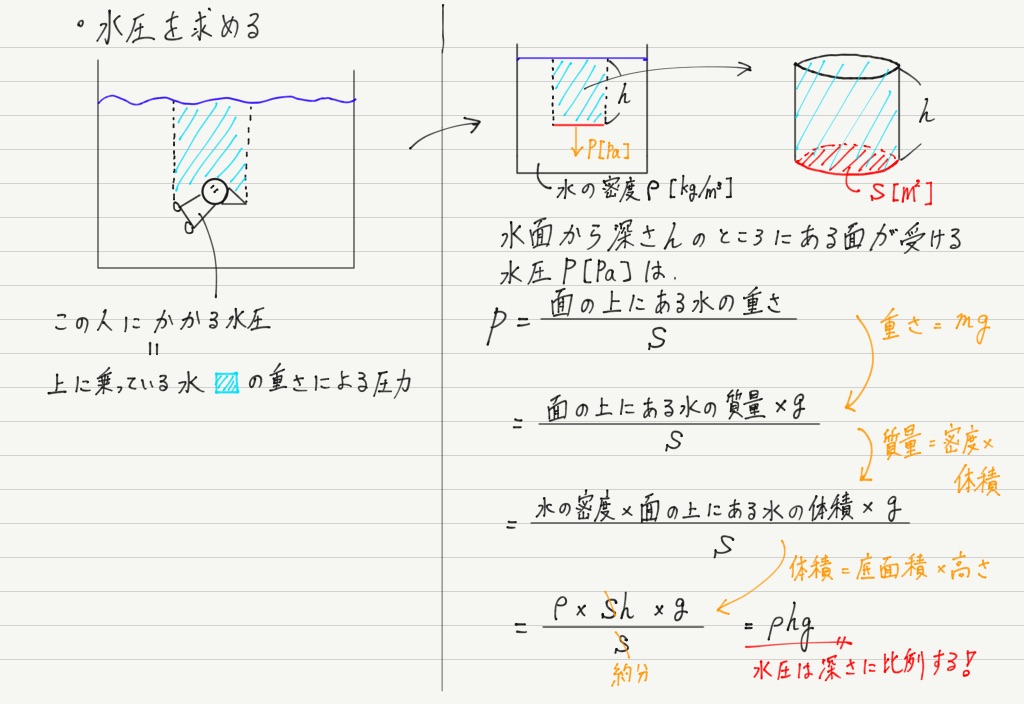



圧力 水圧 浮力 高校物理をあきらめる前に 高校物理をあきらめる前に




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
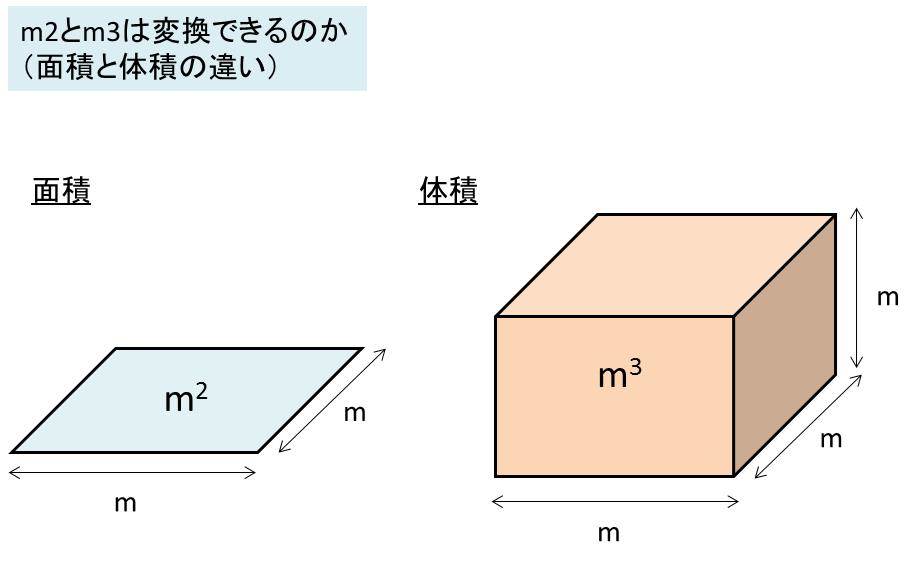



M2 平米 とm3 立米 は換算 変換 方法 計算問題を解いてみよう




体積 表面積まとめ記事 いろいろな図形の求め方を一気に学べる 高校生向け受験応援メディア 受験のミカタ




面積と体積の違い 比較表付き ビジネス 21



1
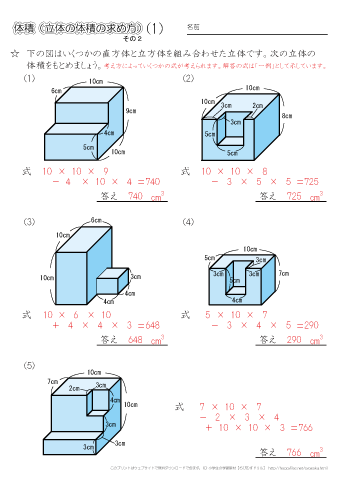



小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生




面積 体積 を英語でなんと言う 数学で使える表現 楽英学




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム
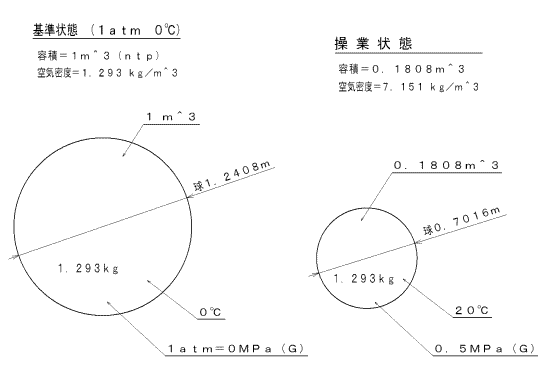



技術資料 気体の流量単位 ボイル シャルルの法則
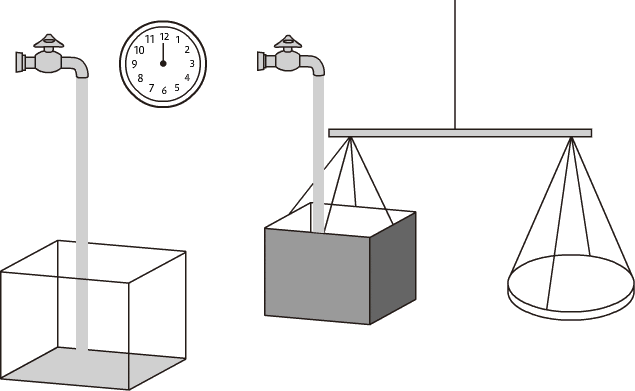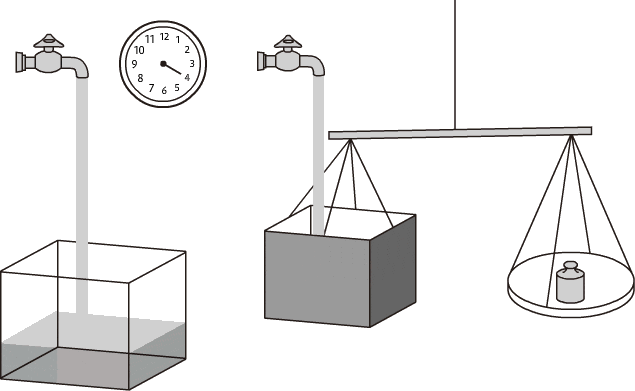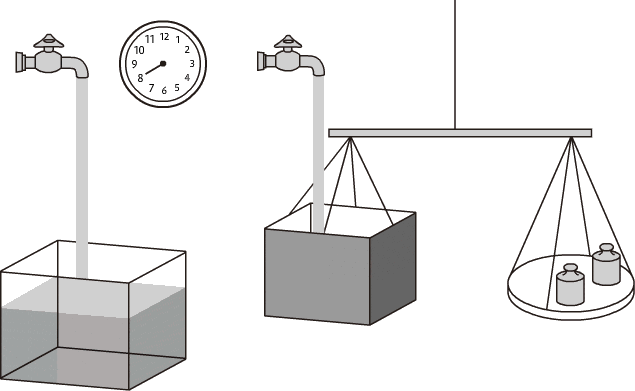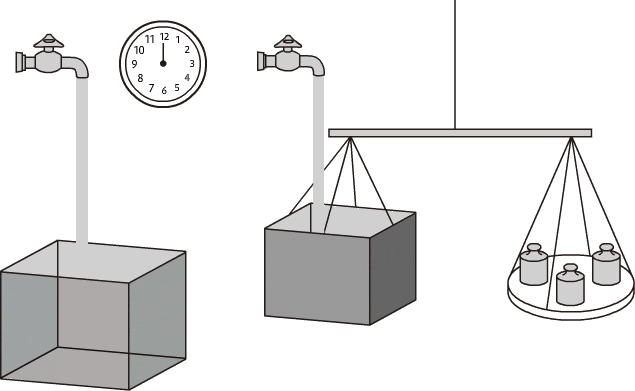



体積流量と質量流量 流量の基本を知る 流量知識 Com キーエンス




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
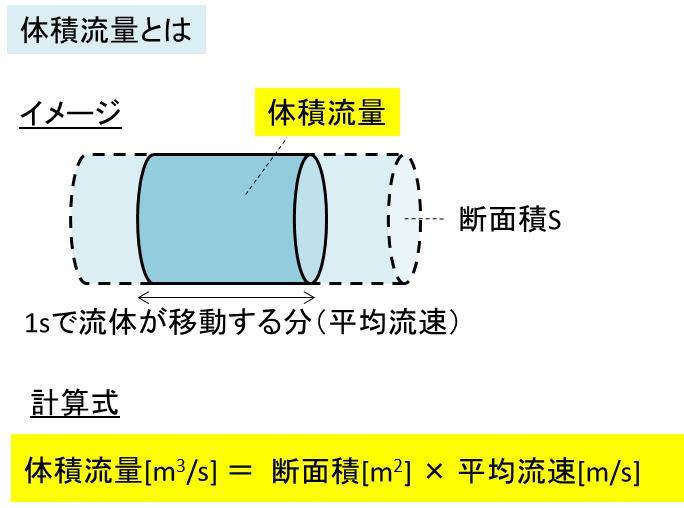



流速と流量の計算 変換方法 質量流量と体積流量の違いは 演習問題




複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座




側面積と表面積と体積の計算の違いがわかりません Clear



コマネチ大学数学科46講 投影図 ガスコン研究所



1
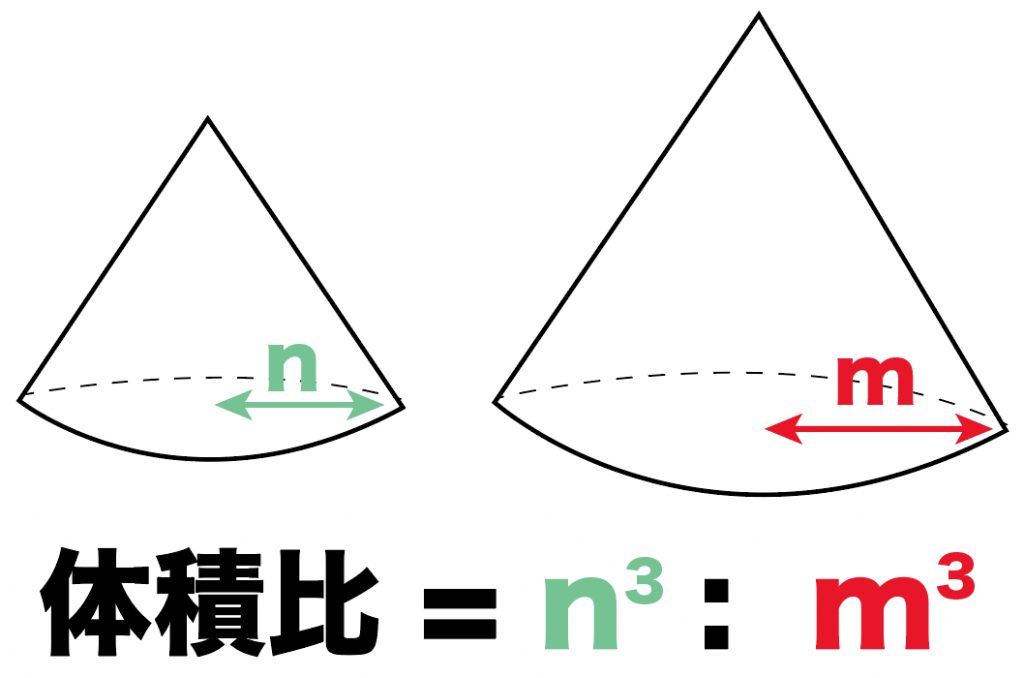



3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく
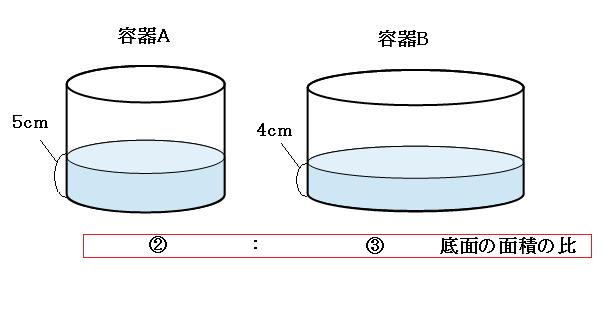



体積と比の問題の解き方 底面積の比と深さの比は逆になる



1
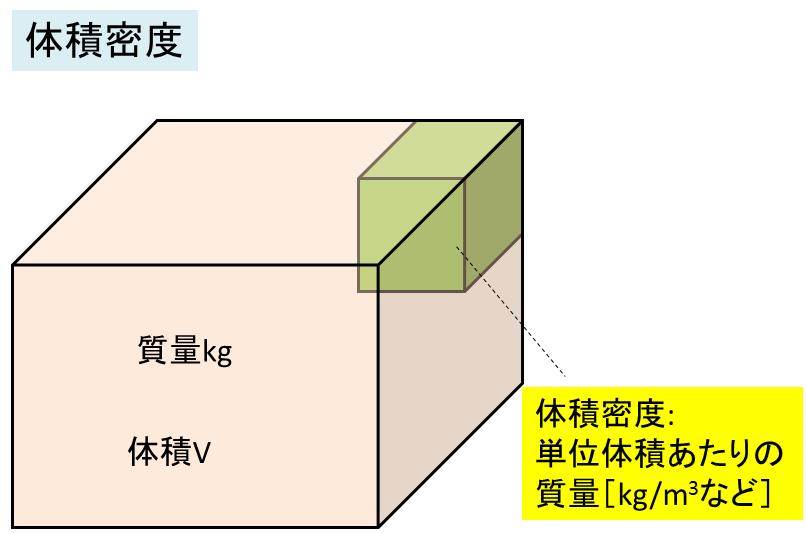



面密度と体積密度と線密度の変換 換算 方法 計算問題を解いてみよう
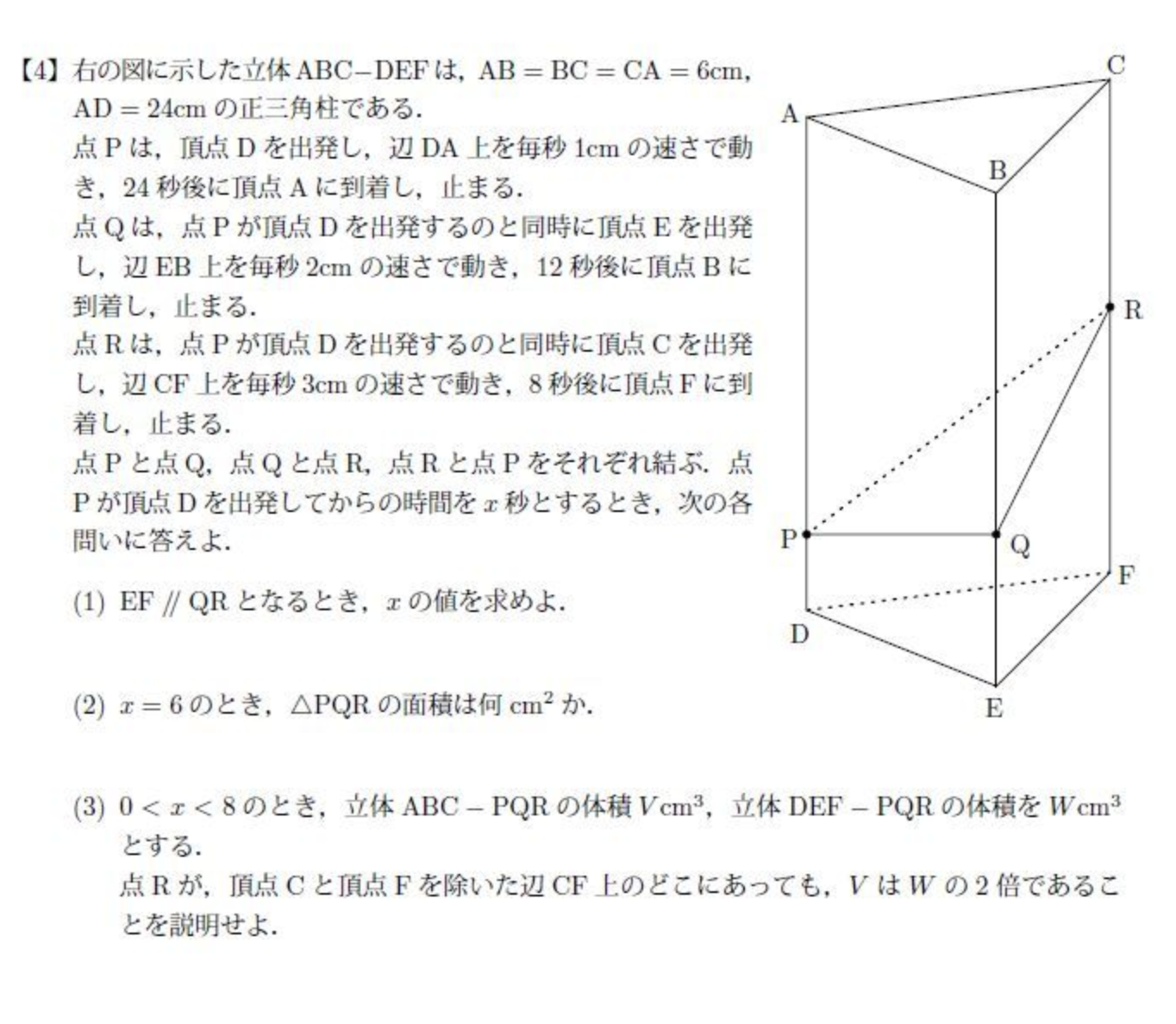



3分で分かる 三角柱の体積 表面積の公式 表面積 をわかりやすく 合格サプリ




長さ面積体積の単位まとめ 家庭学習レシピ
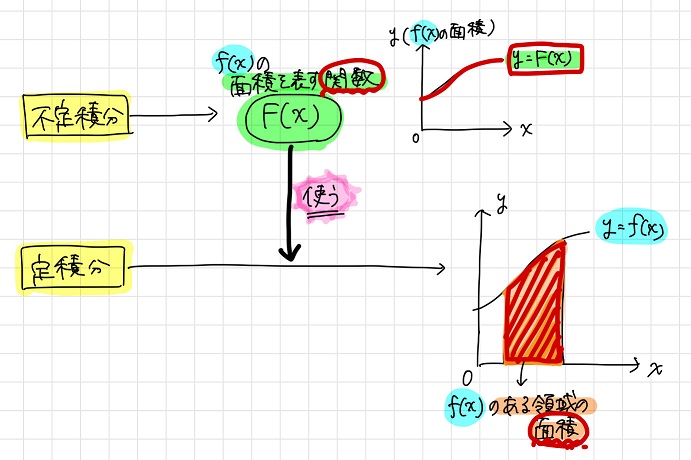



微分積分 定積分と不定積分の違いや関係性 それぞれの特徴とは 積分定数にも着目して解説します 黒豆納豆の特許翻訳



数学の面積と体積の違いはなんでしょうか 面積は平面で体積は立体で Yahoo 知恵袋
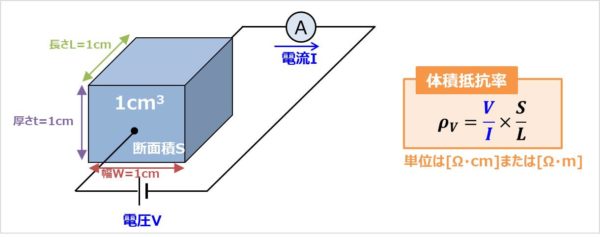



体積抵抗率 と 体積抵抗値 の違い 単位や測定方法について Electrical Information
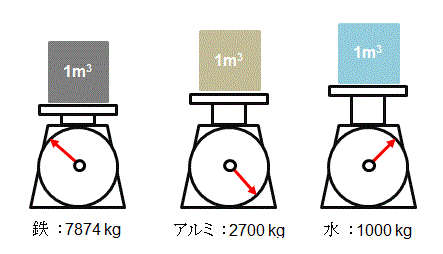



密度と比重量と比重の違い




数学でいう 容積 容量 体積の違いを教えてください Clear




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾
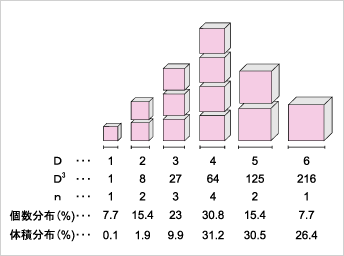



粒子径測定における個数分布と質量 体積 分布との違いとは 技術情報 技術情報 アプリケーション




公式を図解 すい体の体積 円すいの表面積の求め方




体積の求め方 計算公式一覧




体積 Instagram Posts Gramho Com




容積の求め方 小学生の算数質問ひろば 進研ゼミ小学講座



1
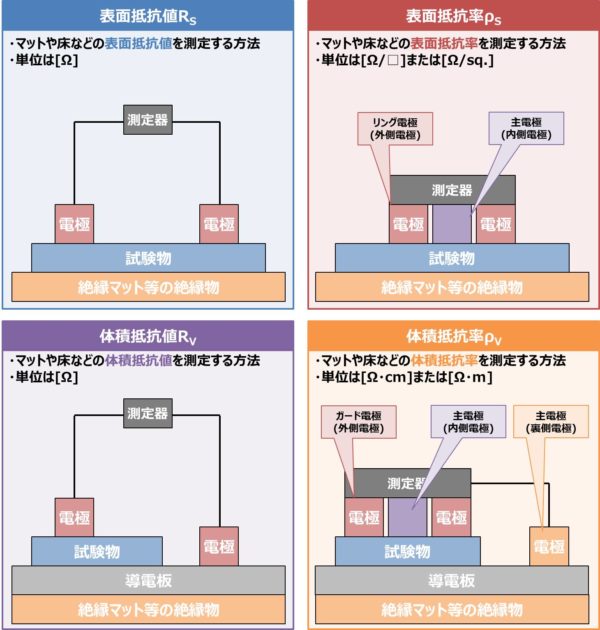



体積抵抗 と 表面抵抗 の違い Electrical Information




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学



面積と体積は 具体的にどのような違いがあるんですか 面積と体積は 具 Yahoo 知恵袋




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題




算数 単位表 時間 長さ 重さ 面積 容積 体積 早見表 即日受取可 雑貨 その他 Omena 通販 Creema クリーマ ハンドメイド 手作り クラフト作品の販売サイト




無料印刷可能 体積 容積 求め 方



5年算数体積2わかる教え方




公式を図解 すい体の体積 円すいの表面積の求め方




小5 算数 小5 7 いろいろな体積の単位 Youtube




側面積と表面積と体積の計算の違いがわかりません Clear




図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト




角錐 円錐の体積と表面積の公式 数学fun




小学生の算数の単位の覚え方は 単位換算表や変換のしくみ 体積 容積の違いも解説 学びtimes



底面積とは 1分でわかる意味 求め方 円錐 三角錐 四角柱との関係 側面積との違い




6 2 図形を1回転させた時の体積比 側面積比 表面積比を求めるには さんすうがく パート 2




数学 中2 13 文字式の利用 面積と体積編 Youtube




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく
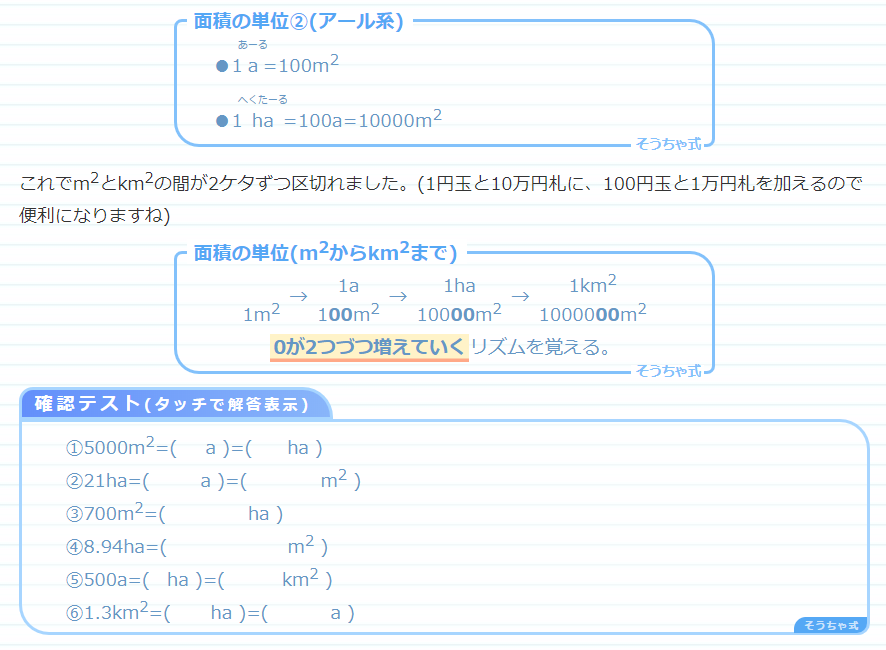



単位の総まとめ 重さ 長さ 面積 体積などの言葉の意味から直し方 計算問題まで そうちゃ式 分かりやすい図解算数 別館
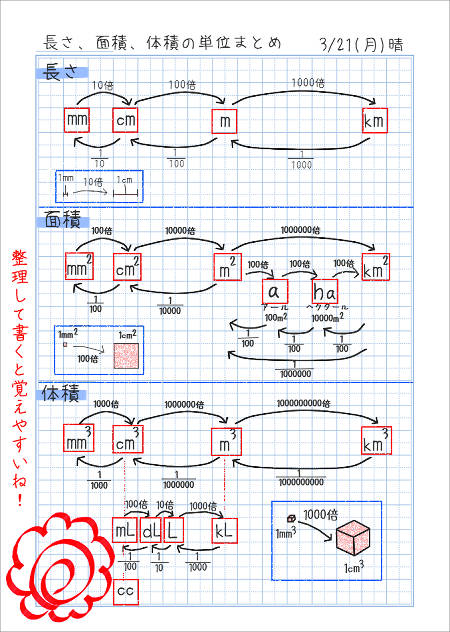



長さ面積体積の単位まとめ 家庭学習レシピ




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




リューベ 立米 とヘーベー 平米 の変換 換算 方法と違いは ウルトラフリーダム
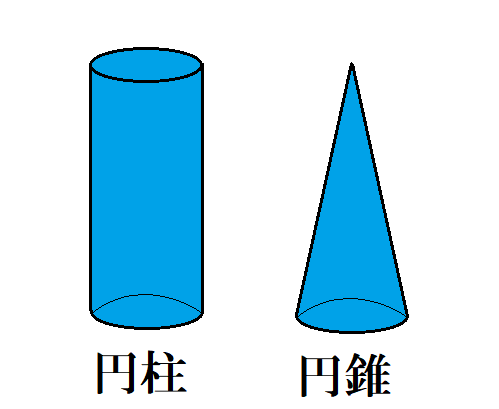



円柱と円錐の違い 表面積や体積 展開図など調べてみたよ ヒデオの情報管理部屋




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ




面積 体積 表面積を教える




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
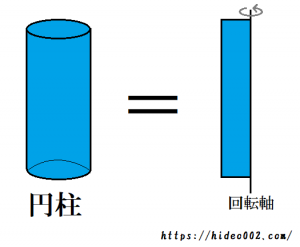



円柱と円錐の違い 表面積や体積 展開図など調べてみたよ ヒデオの情報管理部屋
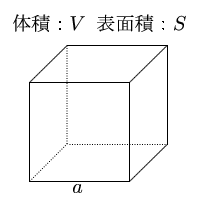



立方体の体積 表面積 体積 表面積の計算 計算サイト




角錐 円錐の体積と表面積の公式 数学fun



かさ 体積 容積のまとめ みけねこ小学校




圧力の公式と単位 水圧の計算もわかりやすく解説 Dr あゆみの物理教室



底面積とは 1分でわかる意味 求め方 円錐 三角錐 四角柱との関係 側面積との違い
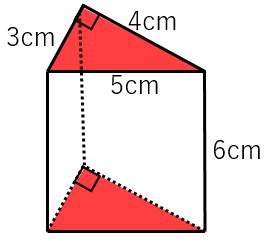



三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学
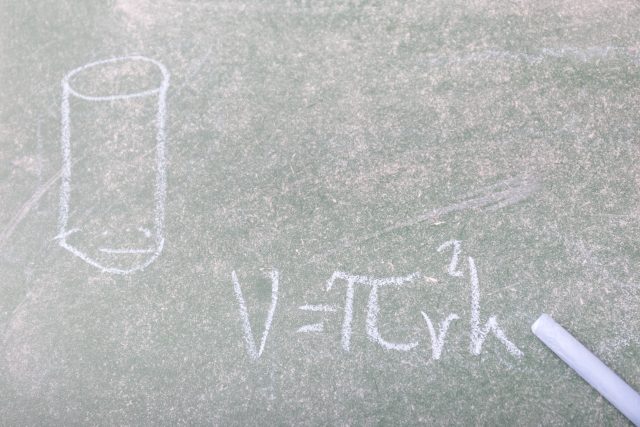



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




小5 算数 小5 3 直方体と立方体の体積 Youtube




面積と体積 単語を比較します 21




圧力の公式と単位 水圧の計算もわかりやすく解説 Dr あゆみの物理教室
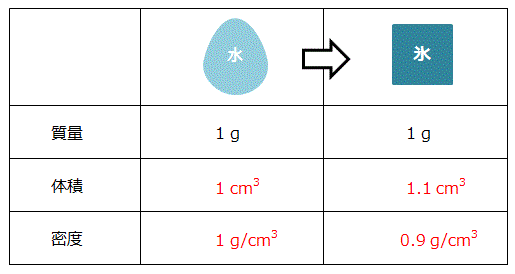



密度と比重量と比重の違い



平米と立米の関係は 1分でわかる意味 違い 変換する計算
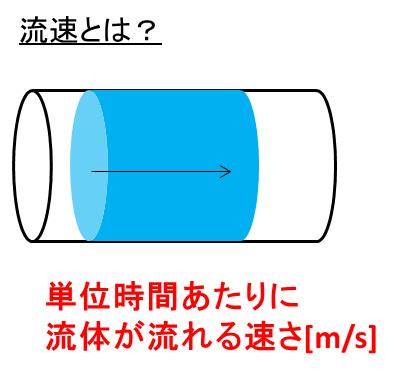



質量流量と体積流量の違いと変換 換算 は 流速と流量の計算方法は 白丸くん



体積 算数用語集




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun



Newみんなの算数講座104 プリン 中学受験の算数知恵宝庫



0 件のコメント:
コメントを投稿