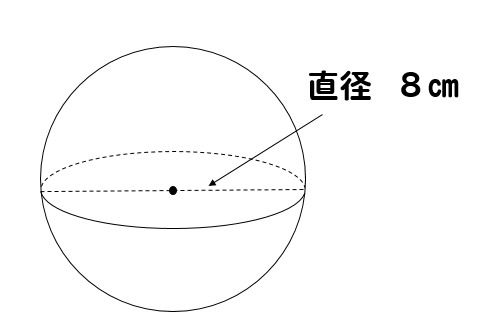
円のように見えないこともないので,この図形を円と捉えることにする. 円の半径=球の周の長さの 1 4 = 1 2πr 半径 1 2πr の円と見立てて面積を求めると, 面積= 1 なぜ球の表面積は なのかを証明しよう。 先ず半径, 中心角 の扇形から, 半径, 中心角 の扇形を引いた面積 は次の式で表される。 半球の表面積 S =球の表面積の半分+半球の切り口である直径4cm(半径2cm)の円の面積であることから S = 4π × 22 × 1 2 + 22π = 8π + 4π = 12π 答え 12π cm² ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方 円柱の体積の求め

球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
球 表面積 求め方 積分
球 表面積 求め方 積分- 円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も! 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!←今回の記事それは、「球の表面積の求め方の公式」 S=4πr×r(rの2乗が表記できないので)、球の表面積を求めるこの公式は覚えてました。 ところが教科書を予習していて見つけた、この言葉 「何々、『球の表面積は、その球がちょうど入る円柱の側面積に等しい
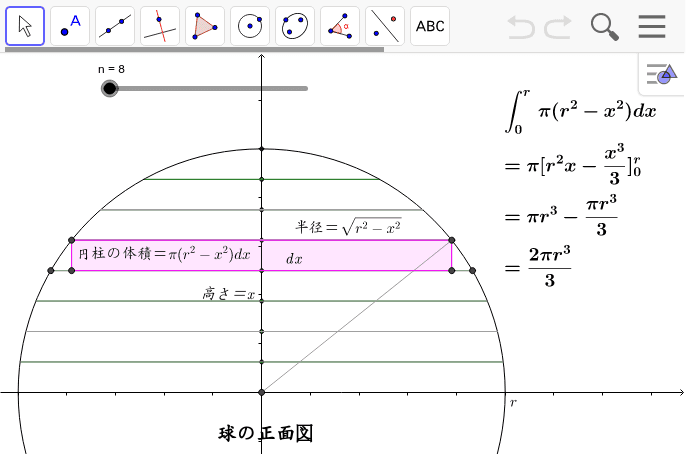



球の体積の積分 Geogebra
半径 r の球の表面積は、次の式で求められます。 球の表面積 \begin{align*} S = 4\pi r^2 \end{align*} 表面積 = 4 × 314 × 半径 × 半径 公式の導出方法と計算例については、「球の表面積の求め方」をご覧 r r の球の表面積は S=4\pi r^2,\ S = 4πr2, 球の体積は V=\dfrac {4} {3}\pi r^3 V = 34 πr3 である。 球を平面で切り取った立体の体積,および側面の面積の求め方を解説します。 結果を覚える必要はありませんが,導出方法はマスターしておきましょう。 目次 球を切って得られる立体の名前 球欠,球台の体積 球冠,球帯の表面積
よって、球の体積Vは、円の面積をx 方向に積分すると、V=2∫0rπ(r2-x2) dxより、 V=2πr2x-(x3/3)0r=(4/3)πr3を導くことができる。 ②球の表面積の公式の求め方(1)例題2:半径が 2 c m の半球の表面積を計算してみましょう。 公式を使うと、 3 × π × 2 × 2 = 12 π c m 2 と計算できます。 円周率 π はおおよそ 314 なので、半球の体積はおおよそ、 12 × 314 = 3768 c m 3 となります。球の表面積がそれに接する円柱の側面積に等しいのは、微小部分を円柱に投影したとき 任意の位置でスライスした(正確な半球でないもの)場合の表面積の求め方 を 上記では、球冠の側面積を重積分で求めたが、高校の数学Ⅲの範囲で十分求め
うさぎでもわかる解析 Part27 2重積分の応用(体積・曲面積の求め方) 19年11月4日 21年7月16日 49分1秒 ももうさ スポンサードリンク こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積(表面積)を求める方法についてまとめてい球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半S:球の表面積ってどうやって求めるのだろう。 s:円の場合は細かな三角形に分割して面積を求めたよ。 円錐の側面積も三角形に分けると簡単に求めることがでる。球でも、同じじゃないかな。 s:そういえば、地球儀を作る時に細かな三角形を張り合わせるでしょう。




球体の表面積 中学生に分かるように真剣に考えてみた うちーノート




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ
1/2時 ・球の体積を求めることができる。 ・球の体積の求め方を理解する。 球の表面積の求め方を復習する。 本時の学習内容「球の体積の求め方を考えよう」を知る。 教科書180ページの「ひろげよう」に取り組む。 何杯分になるかを予想する。 全体ポリスチレン楕円体粒子の表面積計算の為。 259μ㎡でした 9 0507 40歳代 / 会社員・公務員 / 少し役に立った / 使用目的 拝見させて頂きました。 数学難しいです。 この式を見ていたら子供が丁度お薬を飲もうとしていました。 おとうさん娘に教えたいと思っているのが サンタがくるか心配あるので参上! タ(体積) 球の表面積が 出席表に心配あるので事情確認! 表(表面積) どっちも覚えにくいですよね。 球も、表面積の公式を覚えてたら 表面積×1/3×r つまり、表面積を底面、半径を高さとした錐体(頂点がとんがった形)になり
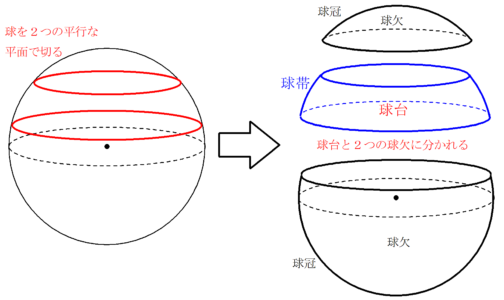



球台と球帯 Fukusukeの数学めも




Mathematics 球の体積と表面積を求める公式 働きアリ
三角柱の体積の求め方は 「底面積 × 高さ」でしたね。 底面積は 4 × 4 × 1 2 = 8 よって、三角柱の体積は 8 × 8 = 64 体積は 64( c m 3 ) となります。 続いて、 三角柱の表面積の公式は 「底面積 × 2 側面積」でしたね。 すると、底面積は先に求めた 8 c m 2 中1数学「球の表面積と体積の定期テスト過去問分析問題」です。 球の表面積と体積の求め方半径rの球の表面積をSとし、球の体積をVとすると、 球の表面積 S=4πr2 球の体積 V=4/3 πr3 (4/3=3分の4)球の表面積と体積の定期球の表面積の求め方 トップページ 合格実績 学年別授業料 戸塚校 講師紹介 3年生用案内 4~6年生用案内 過去問の取り組み 卒業生の声 Q&A プライバシーポリシー 5年算数 プリント&動画 中央林間 4年生の学習の流れ 5年生の学習の流れ



1




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく
球の表面積の求め方の公式を1発でおぼえる方法 球の表面積の求め方の公式である、 4×π×半径の二乗 を一発で暗記してできちゃう語呂を紹介しよう。 このイメージさえ掴んじまえば、テストでも公式を忘れないはず! 球の表面積の公式を暗記するため球の表面積 球の表面積 = 半径×半径×4×314 この公式を,パップス・ギュルダンの定理を利用して,小学生レベルで導いてみます。 パップス・ギュルダンの定理による表面積の考え方 回転させたい図形を, (とても細い)針金でできていると考える立体角は、半径1の球(単位球)の一部の面積で定義されていました。単位球の表面積は $4\pi$ なので、立体角は、$0$ 以上 $4\pi$ 以下です。 「$4\pi$ ステラジアン」は「全方位」に対応する立体角です。 立体角の計算例




球の表面積の求め方 その3 感じる科学 味わう数学
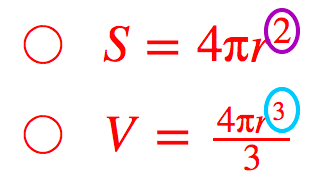



球の表面積と体積の求め方 苦手な数学を簡単に
球の表面積を求める公式は、次の通りです。 S = 4πr2 S = 4 π r 2 ここで、S は球の表面積、π は円周率、r は球の半径を表します。た円の面積や球の体積・表面積を求めるための公式と して生徒は受け止め,これらの式を暗記すればよいと みる傾向が強い。 円の面積,球の体積や表面積の公式を導く過程には, 様々な数学的なアイデ※ 球の表面積は円の面積の4倍になる.(非常にきれいな関係) ※ 高校数学IIIで微分を習えば,体積 V= πr 3 を半径で微分すると表面積 S=4πr 2 になることが分かる.脱線ついでに言えば,円の面積 S=πr 2 を半径で微分すると円周の長さ L=2πr になる.




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
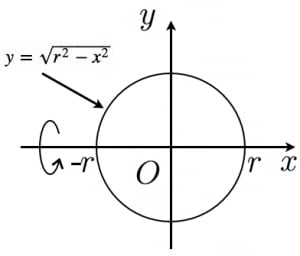



球の体積と表面積を積分で証明 高校数学の美しい物語




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく




球の体積 球の表面積の公式の導出 積分 優技録



ベクトルポテンシャル補足 12 での 球の表面積 を求める証明 Jo3krpの独り言



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



球の表面積の公式の求め方




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




球の表面積と体積の公式 数学fun




球表面積積分 球的表面積的求法 Dycvi




初等幾何 球の表面積を求める 大人が学び直す数学



Math 球の体積と表面積を求める公式 働きアリ The 2nd



球の表面積の計算 もう一つの方法



球欠 球台の体積と球冠 球帯の表面積 高校数学の美しい物語




球の表面積と体積の求め方 苦手な数学を簡単に




球の表面積と体積の公式 数学fun




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



数学 球の表面積を積分で計算してもうまくいかない人へ




球の体積と表面積 Youtube




球の表面積と体積の公式 数学fun



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




初めて知った 球 の表面積の秘密 数学の美しさ 花と器 Coffee Break100のブログ




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



研究




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




球の表面積と体積の公式 数学fun




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




球の表面積の求め方 公式と計算例



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス
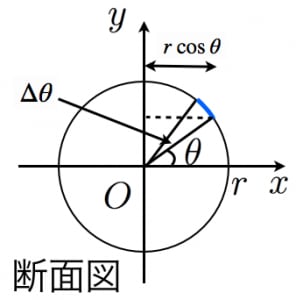



球の体積と表面積を積分で証明 高校数学の美しい物語
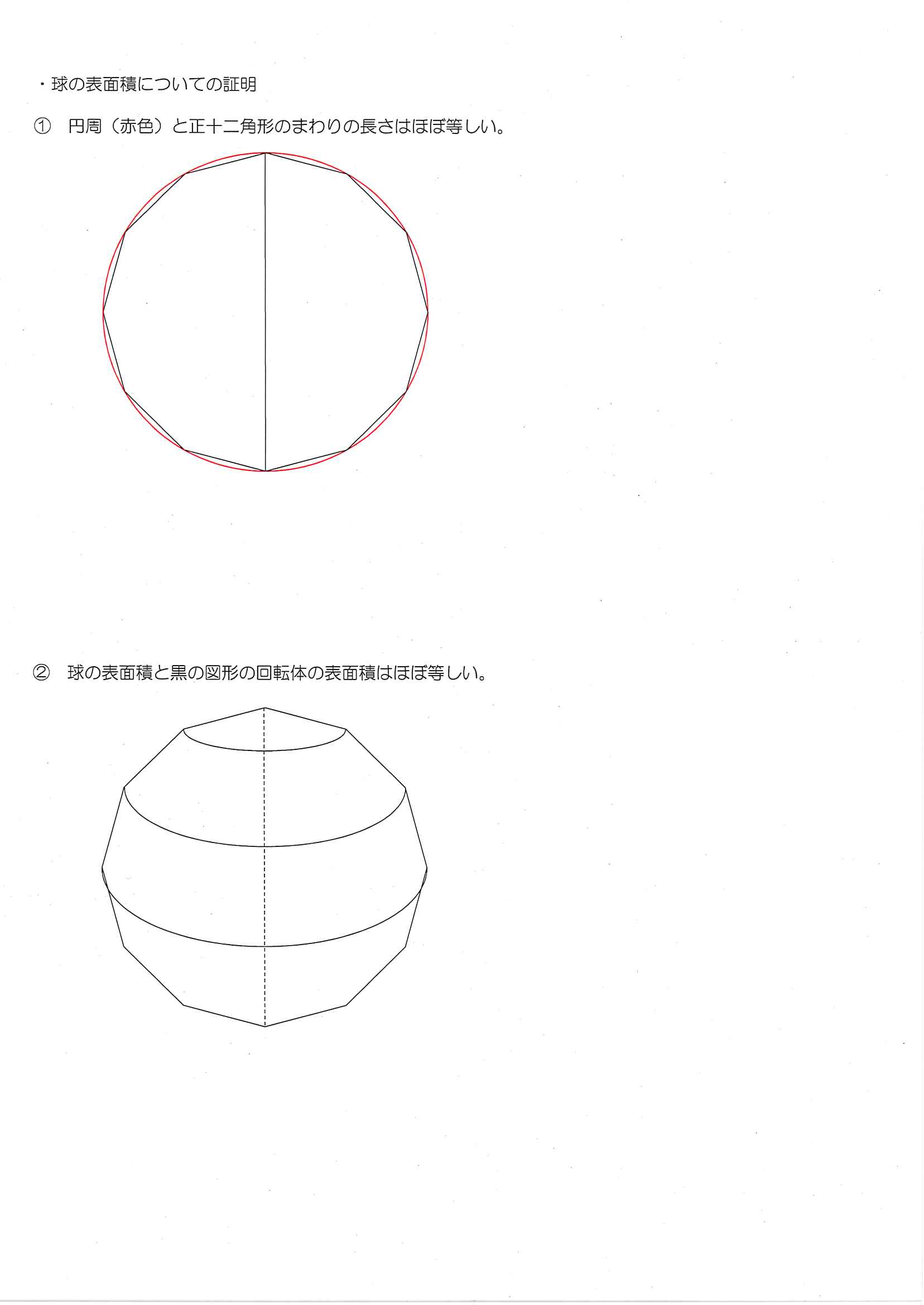



球の表面積の求め方 中学受験塾act アクト のブログ




回転体の表面積 側面積 身勝手な主張



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




初めて知った 球 の表面積の秘密 数学の美しさ 花と器 Coffee Break100のブログ



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




球体の表面積 中学生に分かるように真剣に考えてみた うちーノート




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の体積の積分 Geogebra




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



球の表面積の公式の求め方
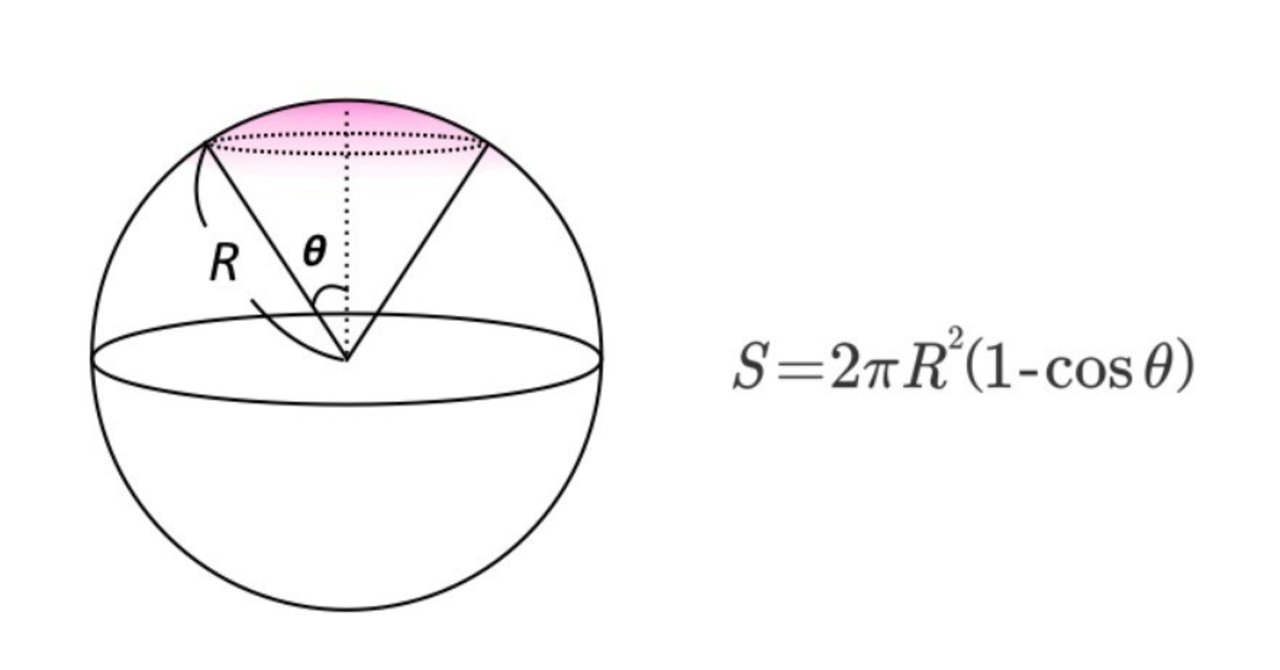



28で見込む部分の球の表面積の計算 Matsubayashi Note




球の表面積と体積の公式 数学fun




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の表面積と円の面積 球の表面積や円の面積を積分により求める場合 パラメ Okwave




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



球の半分と円錐を組み合わせた立体です 体積と表面積を求めよ 教え Yahoo 知恵袋




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題




球の体積公式の微分が表面積になっている理由 Youtube



1




半球の体積と表面積を計算する 具体例で学ぶ数学



球の表面積と体積 計算ドリル 問題集 数学fun
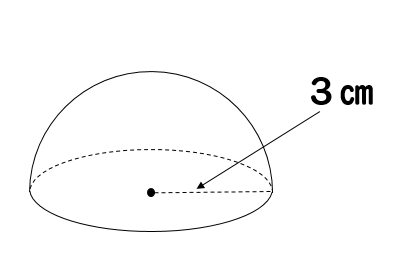



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




球体の表面積 積分で求める方法 うちーノート




球体の表面積 積分で求める方法 うちーノート



1




球の体積と表面積 公式と計算問題と証明 Irohabook



3




定積分と面積3 球の表面積 Youtube




球の表面積 体積 身勝手な主張
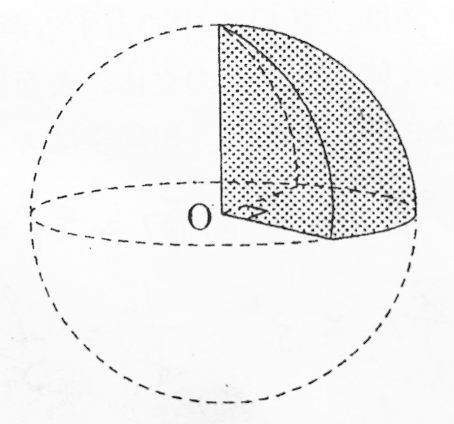



球の問題 苦手な数学を簡単に



数学 球の表面積を積分で計算してもうまくいかない人へ




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




球の表面積の公式について みたにっき はてな




球の表面積の公式について みたにっき はてな




球の表面積 体積 身勝手な主張




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ
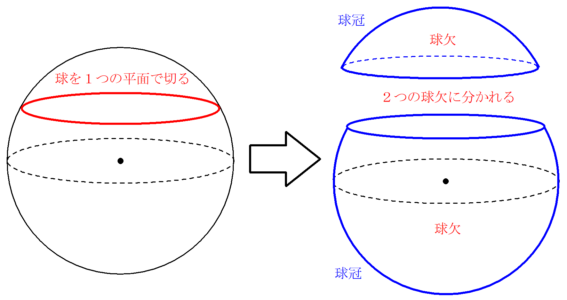



球欠と球冠 Fukusukeの数学めも




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




中1数学 球 例題編 映像授業のtry It トライイット




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




球の表面積と体積の公式 数学fun
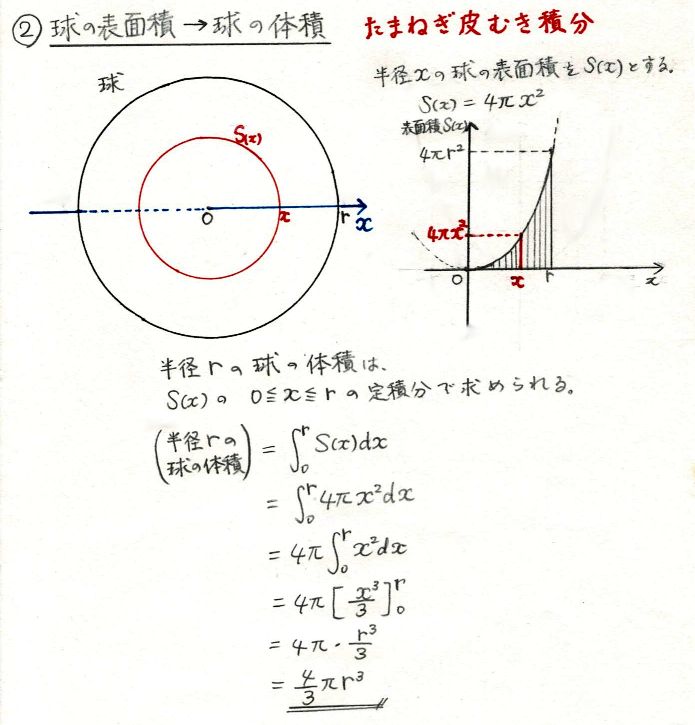



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




球体の表面積 中学生に分かるように真剣に考えてみた うちーノート




中1 数学 6 5 球の体積 表面積 Youtube




球の表面積と体積を求める方法 中学数学 By じょばんに マナペディア




球帯の定理 感じる科学 味わう数学
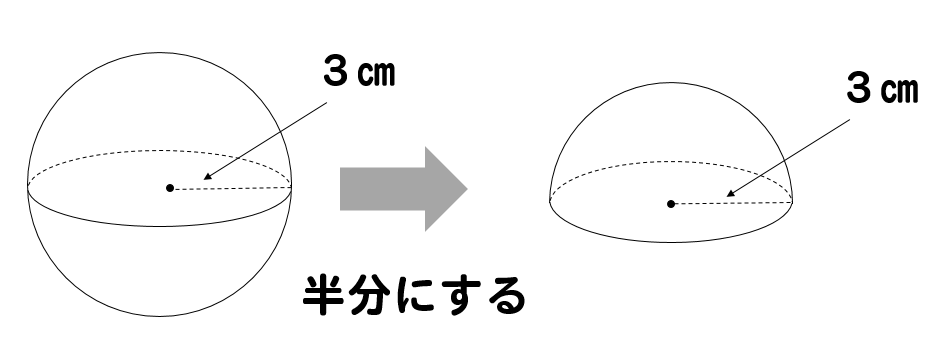



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



球帯と球冠



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



球体の表面積を 積分で求めて下さい 塾で積分を習ったのですが そのとき 球 Yahoo 知恵袋




球の表面積と体積の公式 数学fun



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



球の表面積 体積の教え方



至急 球を4等分したものの体積と表面積の求め方をを教えてください Yahoo 知恵袋



大学入試問題



0 件のコメント:
コメントを投稿