円 面積計算 公式 求め方 計算方法 直径 半径 自動 円周率 計算機 履歴機能付き(2)において,点 (a , b) を中心とする半径 r の円の方程式が (x−a) 2 (y−b) 2 =r 2 点 (−a ,−b) を中心とする半径 r の円の方程式が (xa) 2 (yb) 2 =r 2 点 (a ,−b) を中心とする半径 r の円の方程式が2.遠心力の公式 図のように、 半径r mの円上を、質量m kg・速度v m/sで等速円運動している物体で考えると、 向心力 = mrω2 = でした。 よって、遠心力の公式は、 遠心力
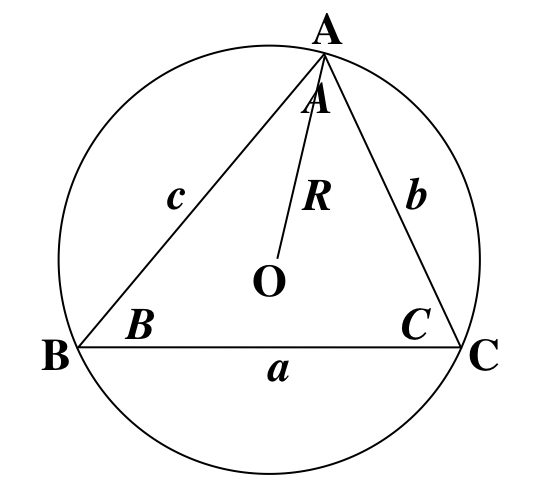
正弦定理とその証明を勉強しよう スタディクラブ情報局
円の半径 公式 高校
円の半径 公式 高校-円の方程式 中心:原点,半径:r の円の方程式 ;図より、底面の円の直径が 8cmだから、半径は4cm底面の円の面積は、4×4×π=16π㎡ 高さは 5cmなので、16π×5=80π㎥ ※(2)は直径が与えられていることに注意!半径は直径の半分! 円柱の体積の公式 V=πr 2 hって?




Math 円 5 直角三角形に内接する円の半径 働きアリ
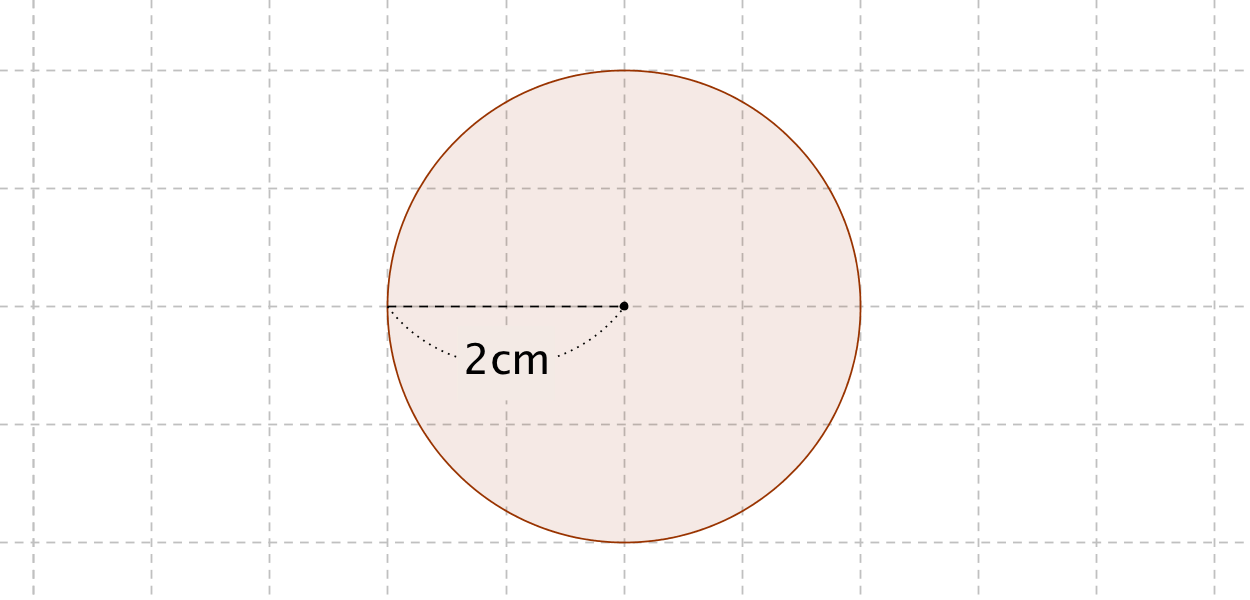
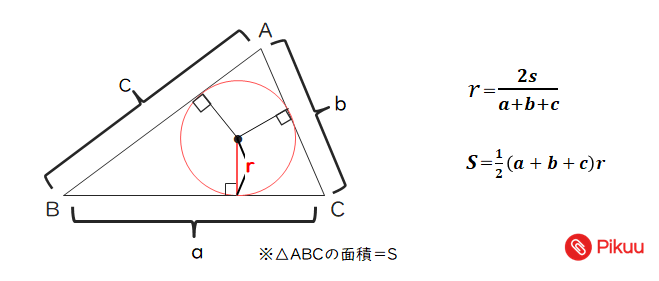
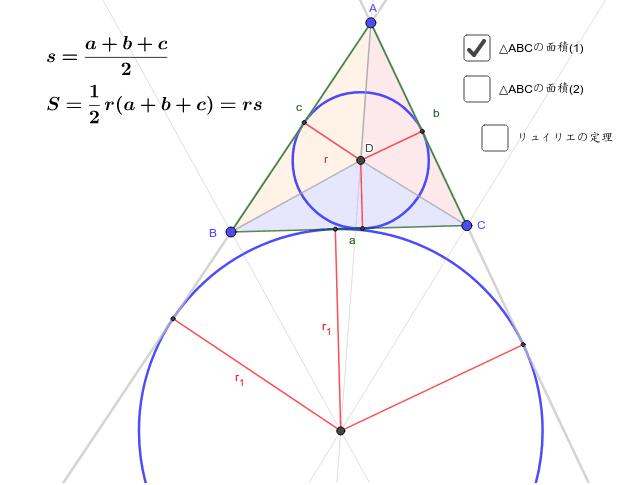
あとは,内心の場合と全く同様にして以下の公式が導けます。 性質1': S=\dfrac {1} {2}r_A (abc)=r_A (sa) S = 21円周率 π )という公式で求めることができます。 例題①半径 2 cmの円の面積を求めて下さい。 答え: 2 ×半径を求めるために、新しい公式を覚えたりする必要はないってことだね! 安心したよ♪ かず先生 そうだね! だけど、計算はちょっと複雑だったりするから たくさん計算練習しておこうね! スポンサーリンク Share this クリックして Twitter で共有 (新しいウィンドウで開きます)
314 = 1256 ( c m) になります。半径ではなく,直径で使えるようになること。 半径を直接測定したり取扱う機会はあまりない。 いちいち半径の公式から換算するのは能率が悪い。 円と球の公式中心:原点,半径:r の円の方程式 x 2 y 2 = r 2 r と θ を使って円周上の点Pを表すと, {x
円の面積と半径の関係は下式です。 A=πr 2 r=√A/π(※√はA/πにかかる) Aは円の面積です。 半径の求め方と公式 半径の求め方と公式を下記に整理しました。半径の記号はrとします。 r=D/2 直径と半径の関係 r=L/2π 円周と半径の関係 r=√A/π(※√はA/πにかかる) 円の面積と半径の関係/ 幾何学 弧長(円弧の長さ)L、弦長d、矢高(円弧の高さ)h、半径rのどれか2つに値を入力して、残りの2つを0と入力すると(空白にはしないでください)、その残りの2つおよび中心角を計算します。 L=r*θ, d=2*r*sin (θ/2), h=r* (1cos (θ/2))を用い、ニュートン・ラフソン法で計算しています。今回は高校数学Ⅱで学習する円の方程式から 『円の方程式の求め方』 について問題解説をしていくよ! 今回取り上げる問題はこちらだ! (1)中心が原点で、半径2の円 (2)中心 で、半径5の円 (3)中心 で、 軸に接する円 (4)中心 で、 軸に接する
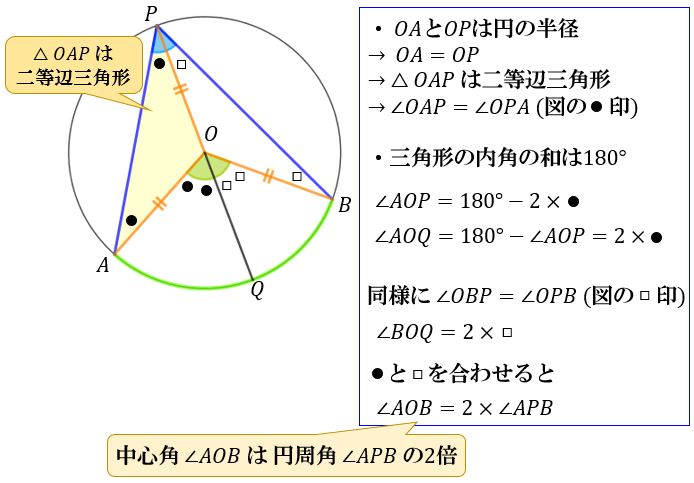



円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ
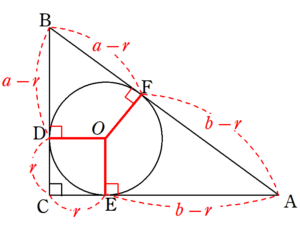



三平方の定理の証明 内接円の利用 Fukusukeの数学めも
押しているあいだ、 の点を持つ円が、円周に沿って回転します。 もとの位置にもどるまでに何回転するか調べてみましょう。回転数は の中に表示されます。 が最初の状態と同じように上を向いたときが1回転です。 (内側を回転するときは下を向いたときが1回転)半径 : π(円周率)=円の面積を求める公式は 円の面積 \(=\) 半径 \(\times\) 半径 \(\times\) 円周率 なので、円の面積を \(S\) とすると \ \begin{aligned} S \ &= 32 \times 32 \times 314 \\ &= \(cm^2) \end{aligned} \ になります。 練習問題③ 面積が (cm 2)の円の半径を求めてください。ただし円周率を 314とします。 円の
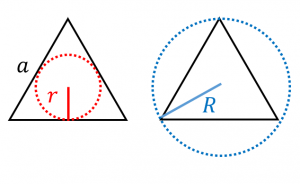



正三角形の内接円の半径と外接円の半径 具体例で学ぶ数学




円の面積はなぜ 半径 半径 3 14 なの 一目で理由が分かるサイトが話題に ねとらぼ
円周率 = 3.14 → π(パイ)と表記します。 半径 = r と表記します。 直径 = 2r (半径の2倍なので)と表記します。外接円の中心を外心 (circumcenter) と言い、その半径を外接半径 (circumradius) と言う。 外接円を持つ多角形は、円 内接多角形 ( inscribed polygon ), cyclic polygon (輪状多角形) あるいは、そのすべての頂点が同一円周上にある(つまり、 共円 である)ことにより 共円多角形 ( concyclic polygon )など円の半径( r adius) 公式の導き方のイメージ この円の面積を求める公式は、円を無限個の扇形に分け、それを長方形につなぎ変えることで導くことが出来ます。 いきなり無限個といわれてもよくわからないと思うので、まずは円を同じサイズの扇形に6等分してみましょう。そして、図の




円の方程式の求め方まとめ パターン別に解説するよ 数スタ
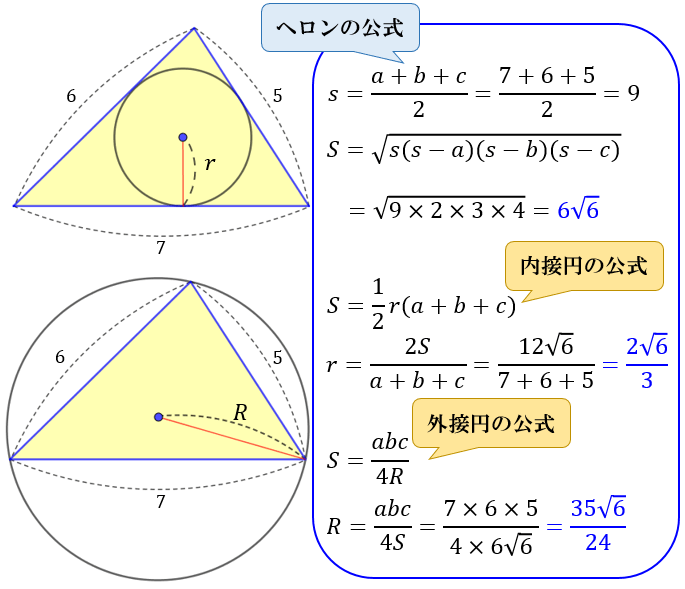



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
名前に「弧」とついているように,円の弧を使って定義します. 弧度法 半径1の扇形の弧の長さが θ であるとき,この扇形の中心角の大きさを θ rad と定める.ただし, rad は「ラジアン (radian)」と読む. 正確には,「円弧と半径が等しいときの中心角正多角形と円/理解シート 円周から,直径・半径を求める方法を教えて 無断複製・転載・翻訳を禁ず gakken bの関係がある 。 周長(円周の長さ) C の円の半径は = で求められる。 正多角形に対しては、単にその半径 (radius) と言った場合には外半径(外接円の半径)の意味である 。 正多角形の内半径(内接円の半径)は辺心距離と言う。 中心を持たない幾何学的対象の場合には、最小包含半径




円の面積 算数用語集




円周の求め方 公式と計算例
X 360 という式を使うことで、 母線の長さ l 、 底面の半径 r 、 側面のおうぎ形の中心角中心:C(a,b),半径:r の円の方程式 (x − a) 2 (y − b) 2 = r 2 r と θ を使って円周上の点Pを表すと, {x = a r cos θ y = b r sin θ となる. (x − a) 2 (y − b) 2 = (a r cos θ − a) 2 (b r sin θ − b) 2 = r 2 (cos 2 θ sin 2 θ) = r 2 原点Oと点Q(a,b)を結ぶ直線OPを直径とする円の方程式 (x − a 2) 2 (y − b 2) 2 = a 2 b 2 4円錐の母線、半径、中心角の関係式とそれぞれの求め方 最終更新日 r = l ×



円の方程式とは 3分でわかる意味 公式 半径との関係
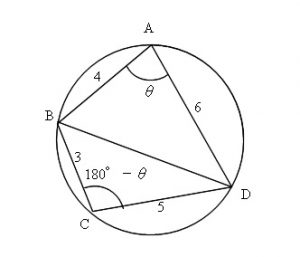



円に内接する四角形の面積の求め方と定理の使い方
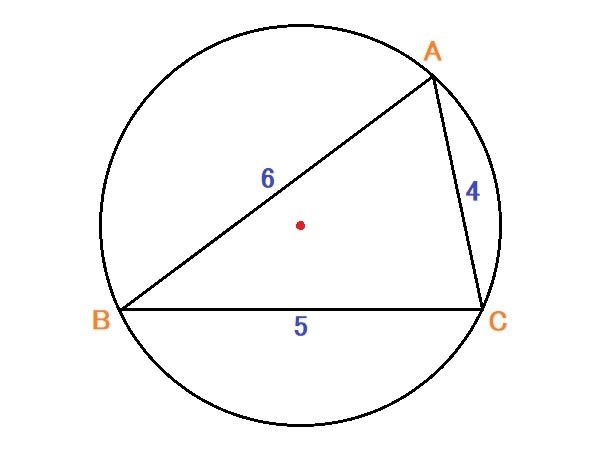
内接円の半径は S=rs によって求められます。ここで面積は、ヘロンの公式によって求めます。 ここで面積は、ヘロンの公式によって求めます。 a=4k , b=2k , c=3k から s= =より 17年10月8日 408 PM おうぎ形の弧の長さは? ken より 17年10月9日 12外接円の半径に関する公式 外接円の半径の長さを求めるのに使う公式は、まずは何といっても 正弦定理 。ただし、与えられる三角形の辺・角の情報によっては、正弦定理だけで解決しないことがあります。




高校数学 内接円の半径の求め方 例題編 映像授業のtry It トライイット




数学ia 三角形の内接円と外接円 大学入試数学の考え方と解法
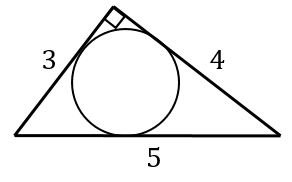
三角形の内接円の半径は公式化されていますが、四角形以上の多角形では別の方法で求める必要があります。 内接円の性質 や、 多角形の性質 を利用して求めることが多いです。一般の三角形の内接円の半径 例題1は直角三角形でしたが,直角三角形でない場合も内接円の半径を計算する場合には,同じ公式 S=\dfrac {r} {2} (abc) S = 2r円の半径 を比べるのです。どういうことか。図を見ればすぐにわかります。 これは直線と円が2点で交わっていますが、このとき 円の中心と直線の距離 \(d\) と 半径 \(r\) はどんな関係になっていますか。そうですね。 明らかに半径のほうが大きくなり
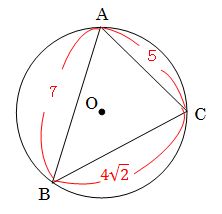



三角形の外接円の半径 正弦定理 図形 センター数学ia対策過去問題集
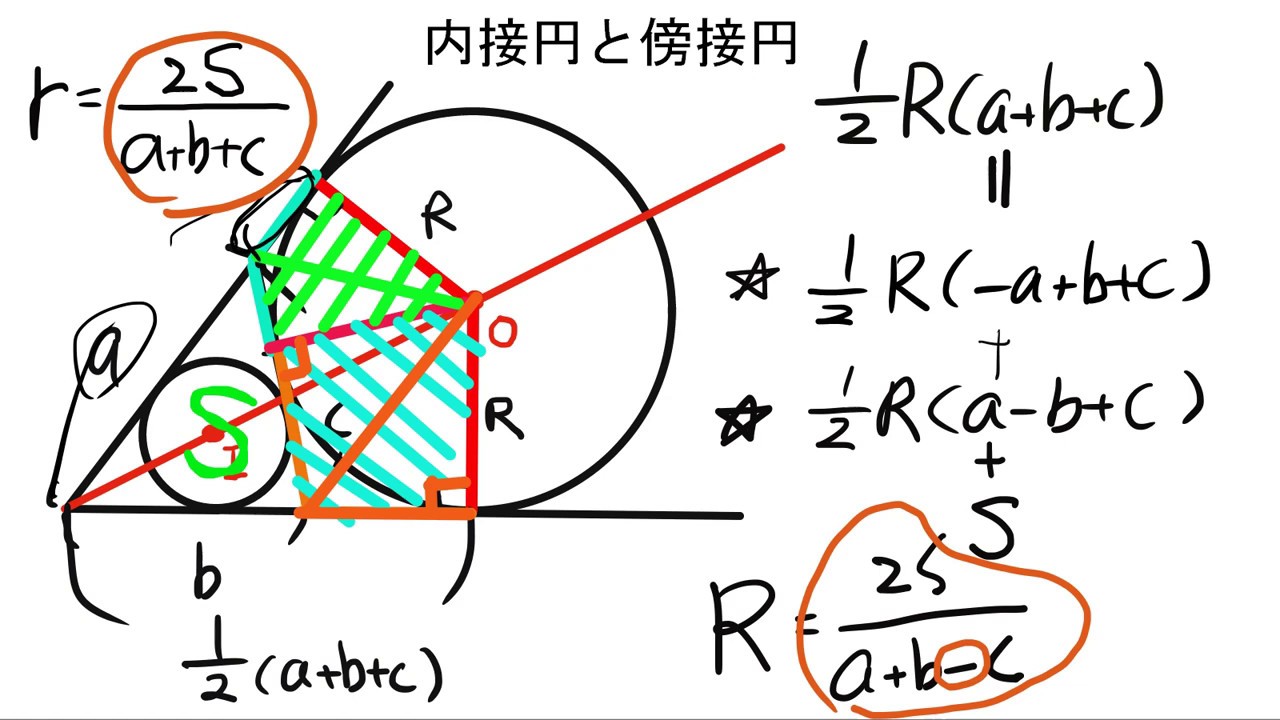



内接円と傍接円の半径公式 Youtube
2つの円の半径 です。例えば円同士が全く交点を持たない場合というのは一つ目に こんなのが考えられます。これは2つの円が 「互いに外部にある」 とよく呼ばれます。この時は見てわかる通り それぞれの中心間の距離よりも2つの円の半径を足したものよりも大きくなっています。 つ円の中心、半径の求め方 中心の座標と半径を求めるためには、円の方程式を次の形に変形する必要があります。 こうすることで、中心と半径を読み取ることができます。 というわけで、円の方程式を変形していきます。 まずは、並べかえて と をまとめます。 次に と について、それぞれ平方完成していきます。 平方完成ができたら、残りモノは右辺に移行し円周の長さを求める公式は、次の通りです。 l = πd = 2πr l = π d = 2 π r 直径d、半径 r の円 ここで、l は円周の長さ、π は円周率、d は円の直径、r は円の半径を表します。 小学生向けに、文字を使わずに書くと次のようになります。 (円周)= (直径)×(円周率)= 2×(半径)×(円周率) 円周を求めるには、この公式に円の直径 d または 円の半径
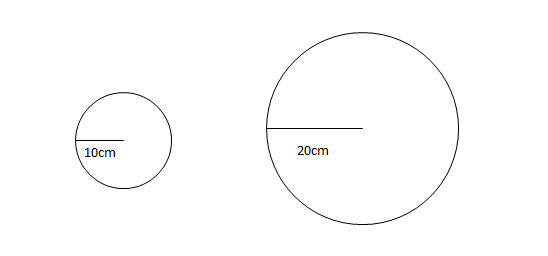



小学算数 円の半径と面積と円周の関係を理解しよう 偏差値40プログラマー




Math 円 5 直角三角形に内接する円の半径 働きアリ
円 周 率 なので、 円周 円 周 = 4 ×公式を使ってみる 図のような二等辺三角形について、内接円の半径を求めよ。 r = 2 S a b c を使うためには、面積 S を計算する必要があります。 この二等辺三角形の高さを h とおくと、三平方の定理より、 h 2 5 2 = 13 2 h 2 = 169 − 25 = 144 h = 12ここでは、三角形の外接円の半径を求める公式について説明します。 外接円の半径の公式には、次の \(2\) 種類があります。 公式①正弦定理から求める




3分で分かる 三角形の内接円の半径の長さの求め方 公式 をわかりやすく 合格サプリ




三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ
314 = 1256 (cm 2)円周を求める公式は 円周 直径 円周率 円 周 = 直 径 ×Title 円内接多角形における面積公式・半径公式・統合公式に ついて (数式処理とその周辺分野の研究) Author(s) 森継, 修一
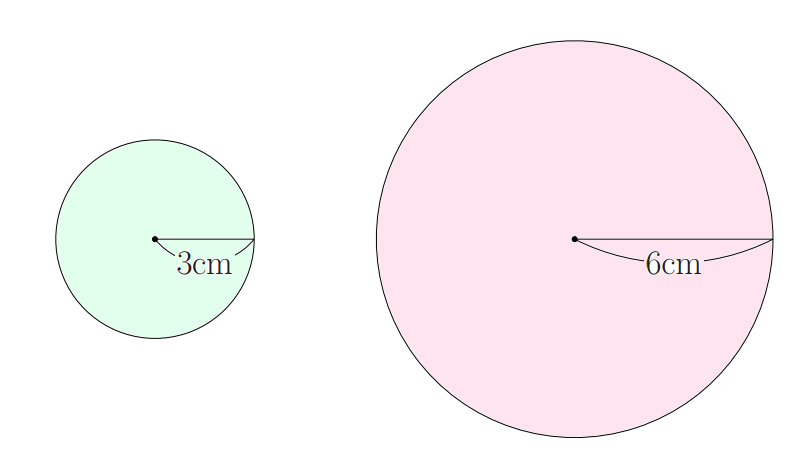



中学数学 2つの円の面積の合計と同じ面積となる1つの円の半径は 偏差値40プログラマー




円周の求め方 公式と計算例
楕円に内接する円の特別な場合として曲率円が考えられる。(→参考:日常の中の曲率) この場合について、上記の公 式を当てはめれば、次の美しい 公式が得られる。 曲率円の半径 r は、 で与えられる。 証明は明らかであろう。それぞれの円の半径と長さと面積を求めよ。 2512㎝ 半径をxcmと置いて、円周の長さに関する方程式を立ててみよう。 半径x2x円周率=円周の長さ ってね。半径がもとまったらあとは円の面積の公式で計算するだけ! (๑>半径を使って円周を計算する公式を書きます。半径は直径の半分の長さですから、直径は(半径×2)と表せます。半径がわかっていたら、次の公式を用いて円周を計算できると覚えておいてください:C = 2πr この公式では「r」は円の半径を表しています。ここ




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく




高校数学 数 97 内接円と外接円の半径 Youtube




正弦定理とその証明を勉強しよう スタディクラブ情報局
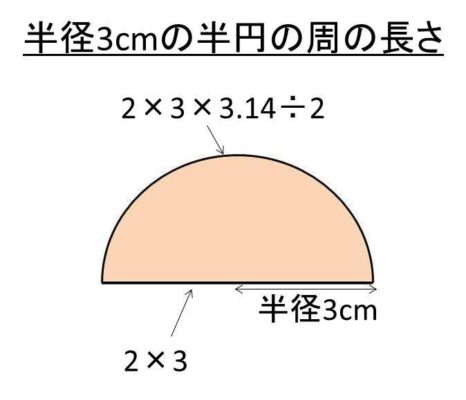



半円の周の長さの計算方法 白丸くん



2 つの円の位置関係 思考力を鍛える数学
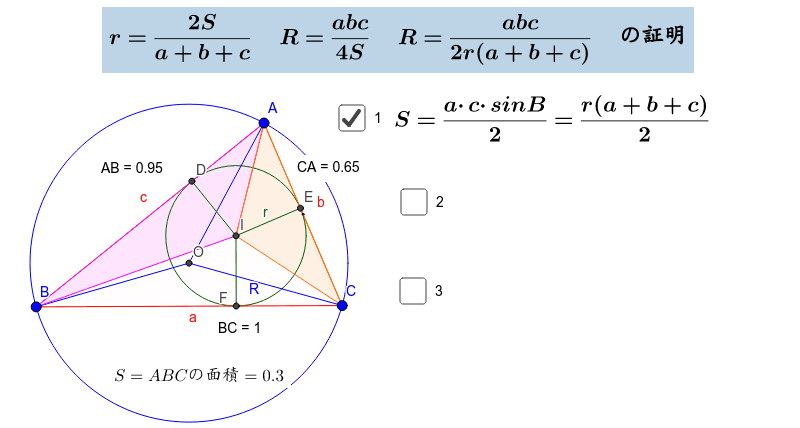



外接円の半径 Geogebra




正弦定理のsina Sincについて なぜsinと言えるのか分かりません Clear
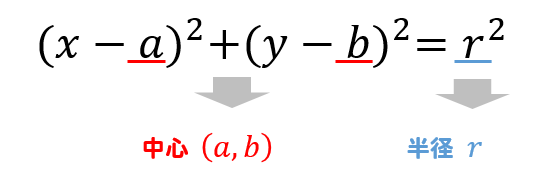



円の方程式 中心の座標と半径の求め方を解説 数スタ



1




中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名




3分で分かる 三角形の外接円の半径の長さの求め方をわかりやすく 合格サプリ
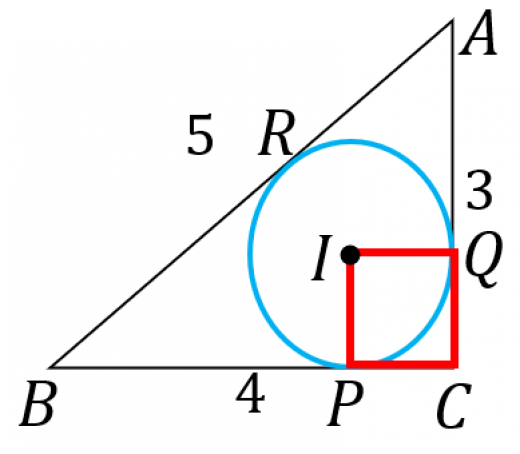



内接円の半径と三角形の面積 高校数学の美しい物語



71 Ab4 5 Ca6 Abc Za Descubre Como Resolverlo En Qanda




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
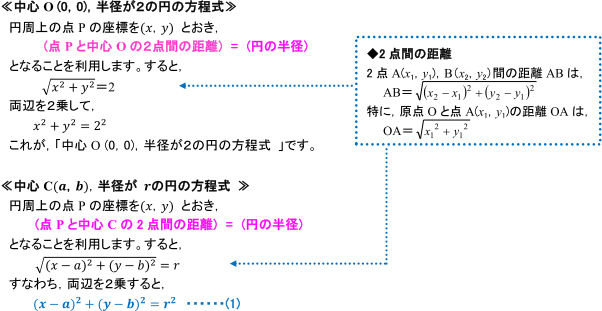



円の方程式の導き方 数学 苦手解決q A 進研ゼミ高校講座



1



中学の範囲で外接円の半径を求める問題で 正弦定理を使わずにどうとき Yahoo 知恵袋
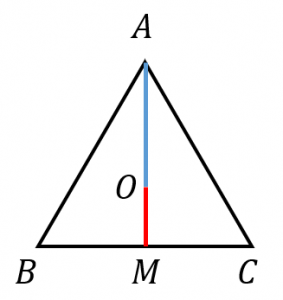



正三角形の内接円の半径と外接円の半径 具体例で学ぶ数学



円の面積の公式 算数の公式
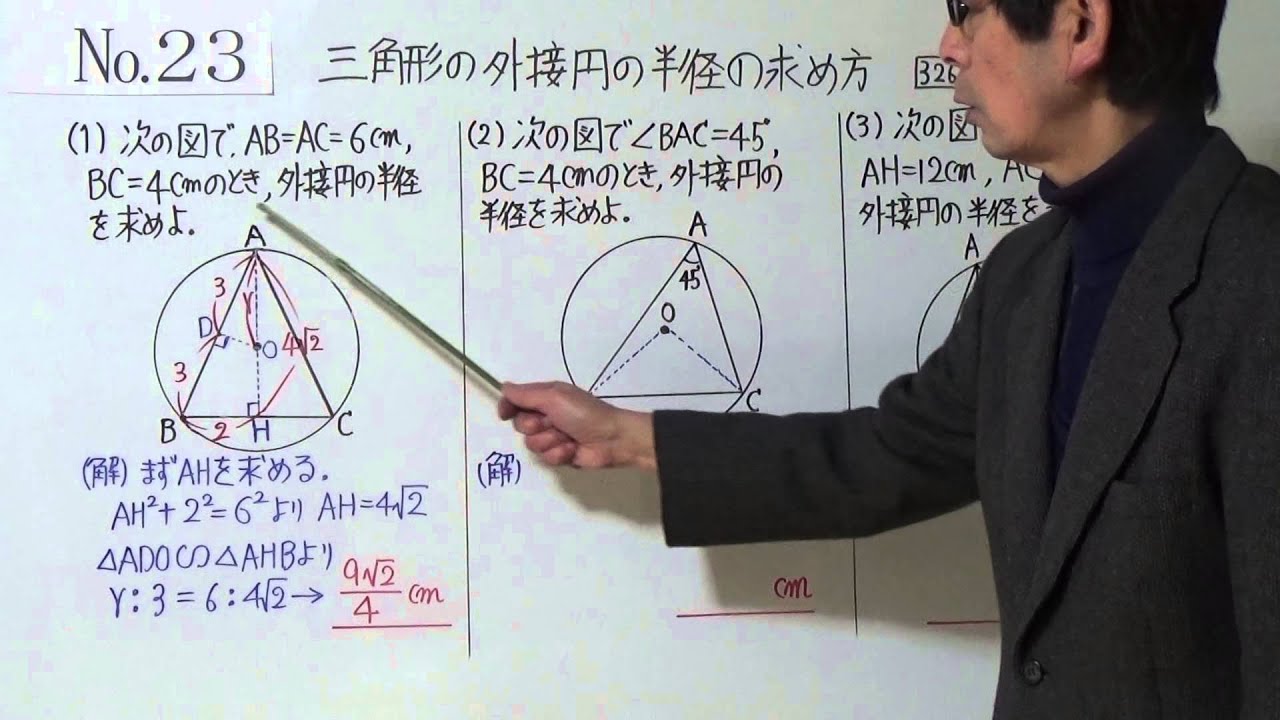



中3 23 4三角形の外接円の半径 Youtube




高校入試数学 外接円の半径に関する対策問題 中学生勉強サイトあかね先生




勉強しよう数学 高校受験用 三角形の高さと外接円の半径rの関係




分からないので式と答えお願いします Clear




数学 外接円の半径 高校入試 正解 名古屋市西区の高校生 中学生向け進学個別指導塾 名学館庄内通校
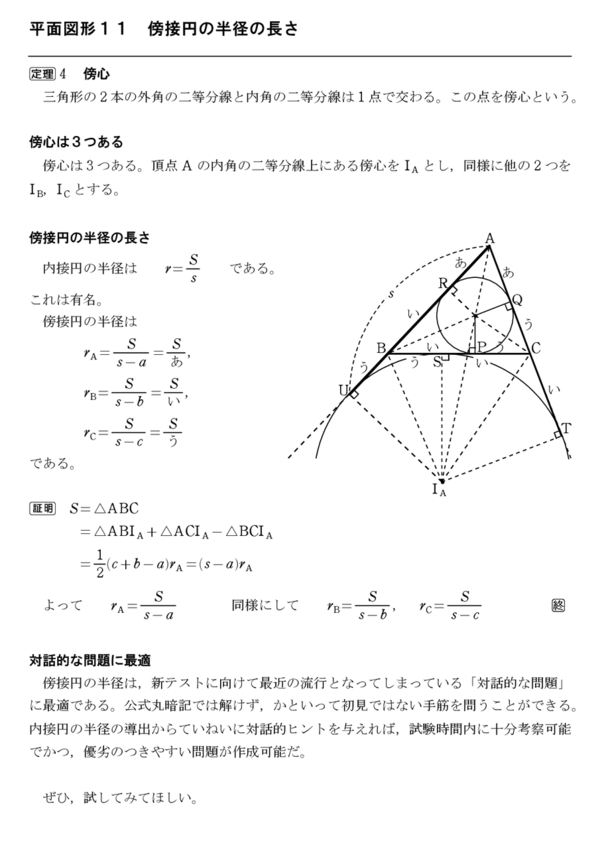



平面図形11 傍接円の半径 怜悧玲瓏 高校数学を天空から俯瞰する
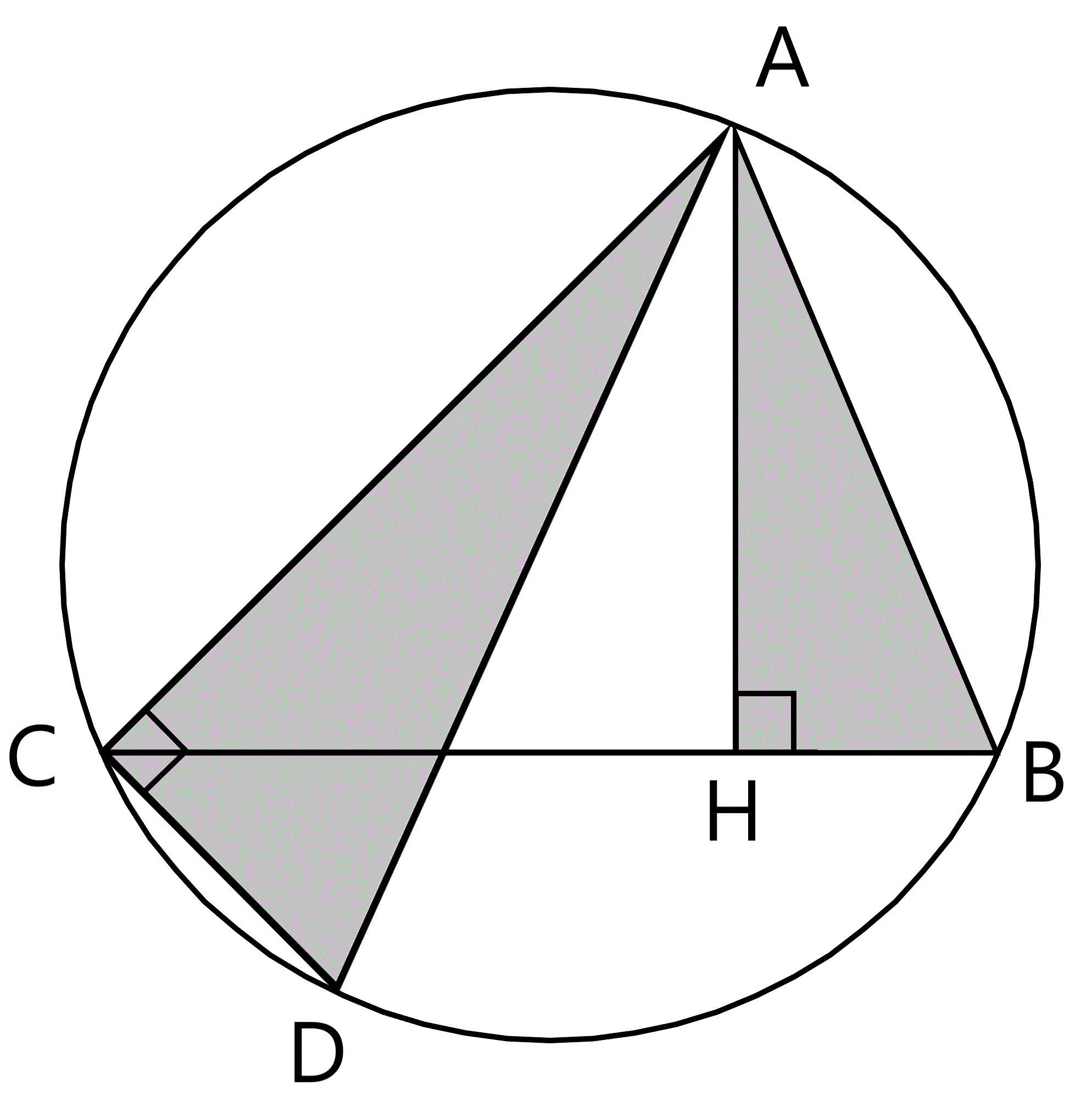



中学数学 外接円の半径の求め方 田中の日記



内接円とは 内接円の半径の公式や求め方 性質 書き方 受験辞典
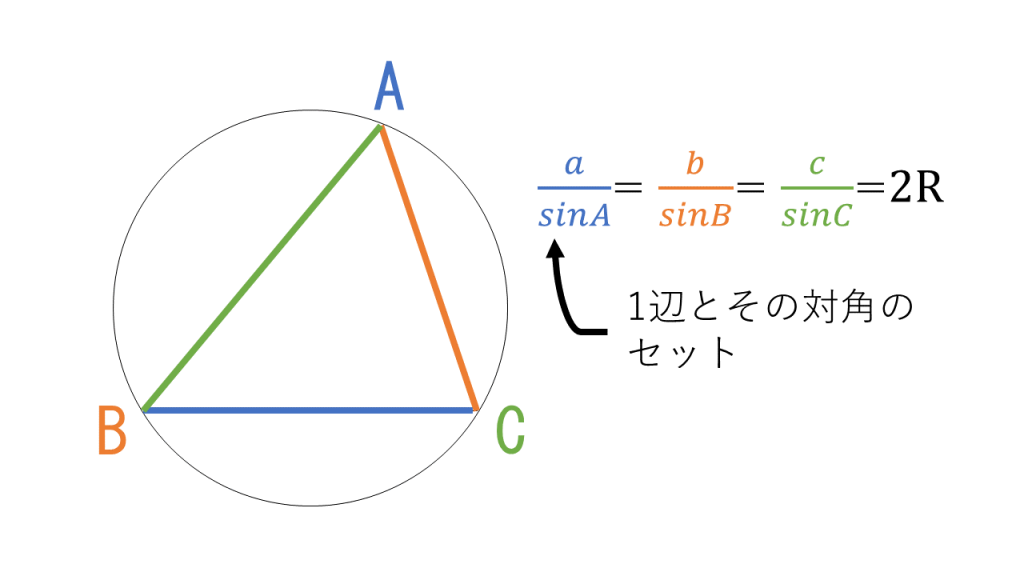



3分で分かる 三角形の外接円の半径の長さの求め方をわかりやすく 合格サプリ




高校数学 内接円の半径の求め方 例題編 映像授業のtry It トライイット




円の面積の公式 算数の公式
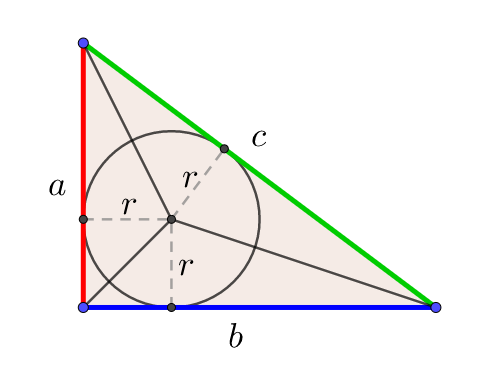



解説 三角錐に内接する球の半径を求めよう 理系のひとりごと




勉強しよう数学解答集 三角形の高さと外接円の半径の関係の証明 その2
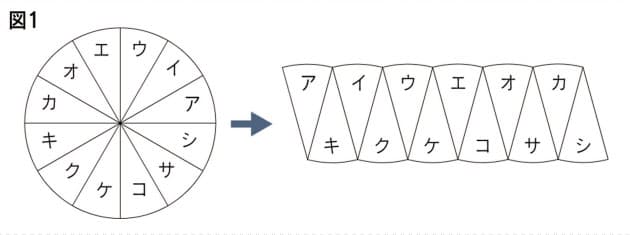



子供に説明できる 円の面積の公式 の証明 Nikkei Style
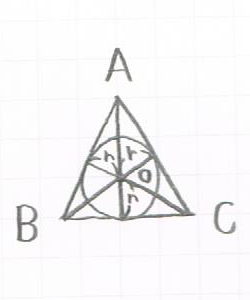



三角形の内接円の半径がわかってるときの面積の求め方




高校数学 正弦定理と外接円 映像授業のtry It トライイット



円の弧 弦の長さで円の半径を求める式をご教示ください 図の弧 弦の Yahoo 知恵袋




三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ




三角形の面積を外接円の半径を使って求める Schoolmath S Diary



高校入試対策数学 三角形に内接する円の半径の長さを求める Pikuu




円 扇形 の面積 周や弧の長さの公式 数学fun




外接円の半径rを三角形の3辺からもとめる Schoolmath S Diary




公式 正弦定理とその証明 数学i By ふぇるまー マナペディア
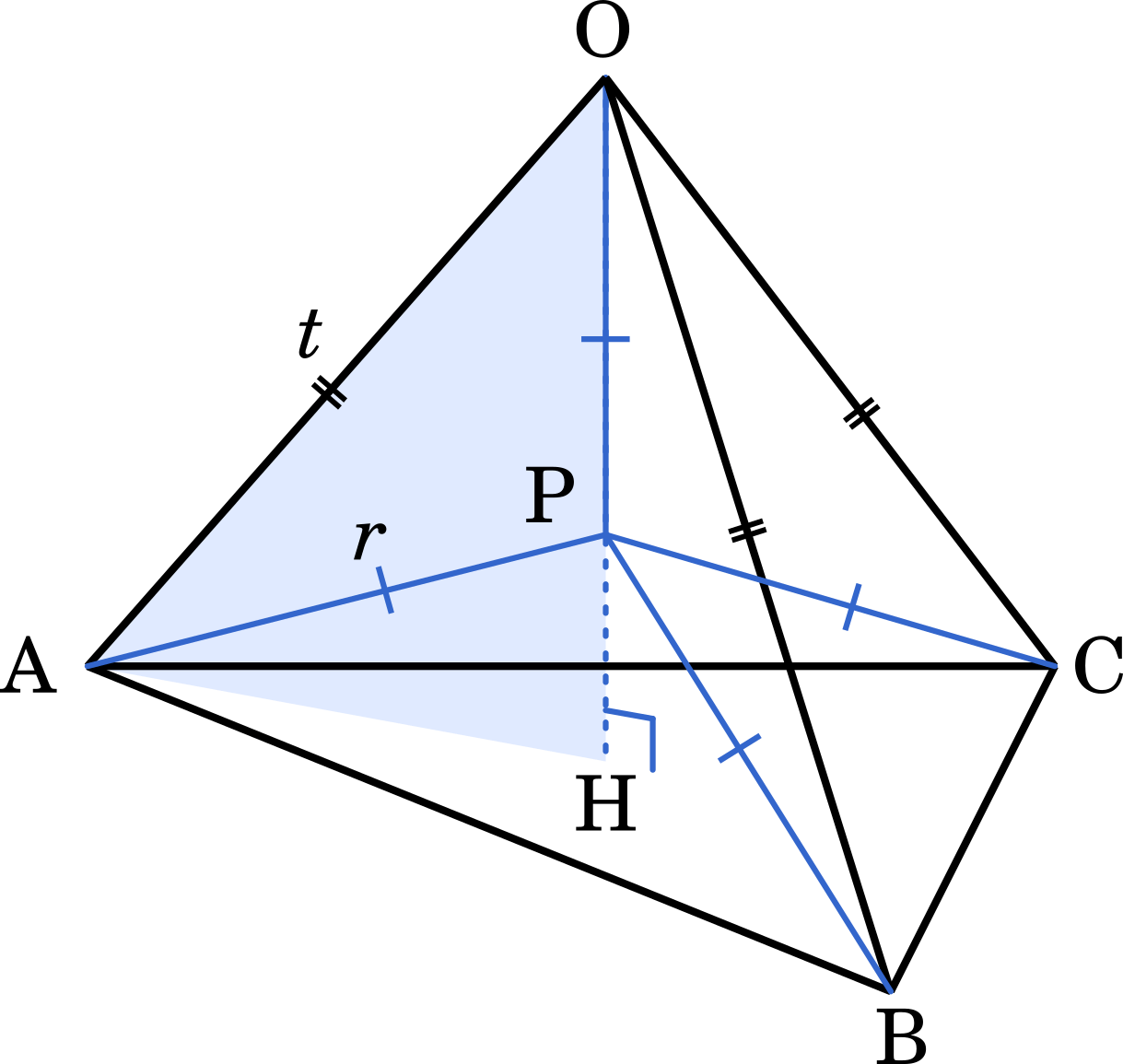



数ia 外接球の半径を考える 千葉大 Mm参考書




高校数学 正弦定理と外接円 練習編 映像授業のtry It トライイット




三角形の外接円の 4 つの性質 証明付 理数アラカルト




正弦定理の指導の細かすぎる工夫3 怜悧玲瓏 高校数学を天空から俯瞰する




円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題




これの外接円の半径の長さの求め方を教えてください Clear



3
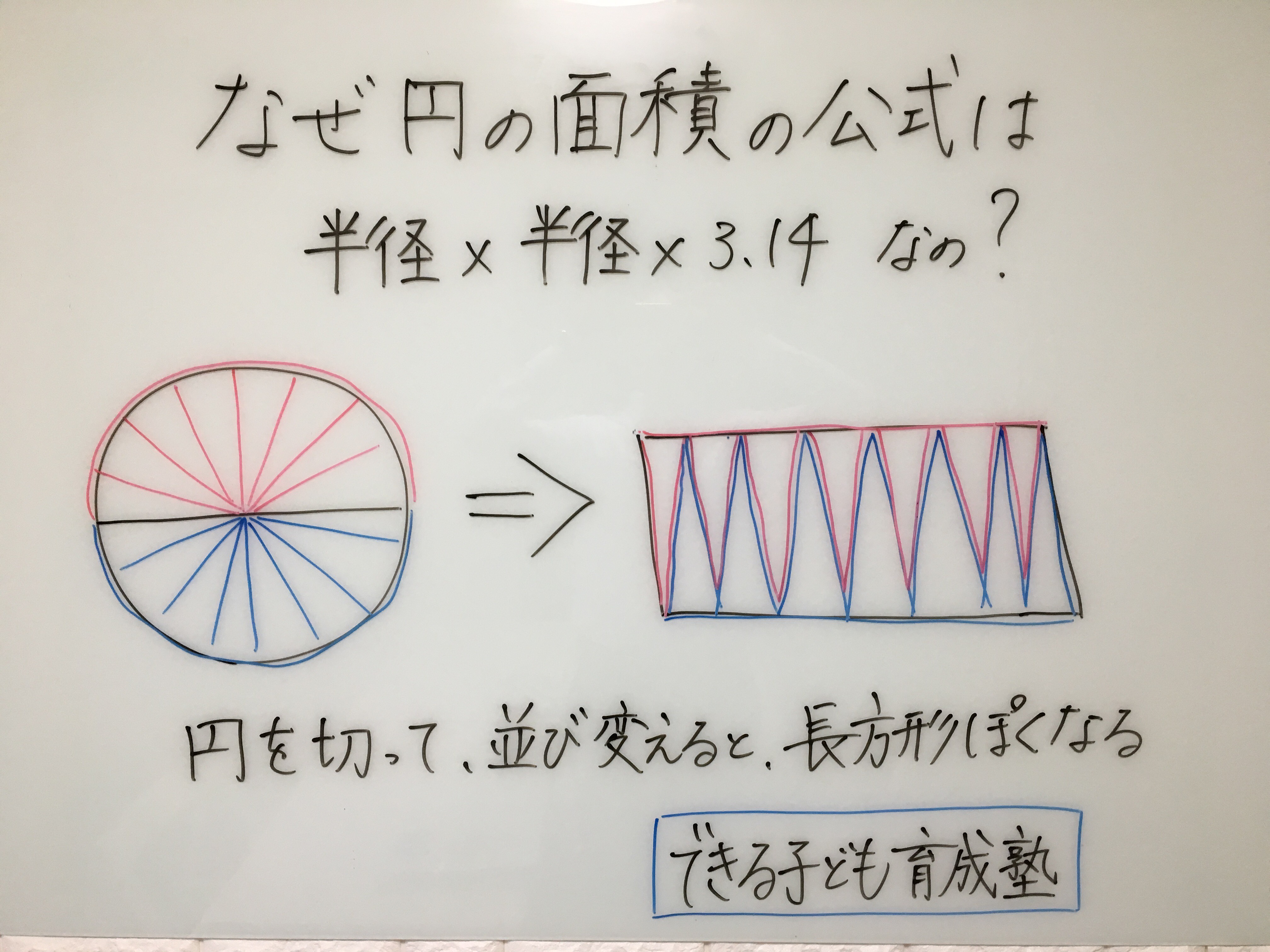



円の面積の求め方 公式 の理由を小学生に教える方法 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の 小学生専門 国語と算数の苦手を克服




円周の求め方 公式は直径を使うので 半径と間違えないように 中学や高校の数学の計算問題




円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト




次のような Abcにおいて 外接円の半径rを求めよ これは学校から配ら その他 教育 科学 学問 教えて Goo




数学 外接円の半径 高校入試 正解 名古屋市西区の高校生 中学生向け進学個別指導塾 名学館庄内通校



外接円とは 半径の公式や求め方 性質 書き方 受験辞典
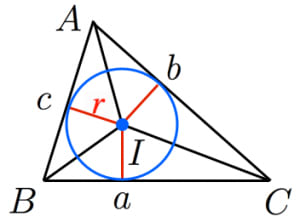



内接円の半径と三角形の面積 高校数学の美しい物語



内接円と傍接円の半径 Geogebra




悲報 教科書の公式は無駄すぎた 内接円 外接円の半径を最速で求める新公式 超わかる 高校数学 Youtube



外接円の半径の求め方 Menkarm World



内接円の半径を求める公式 具体例で学ぶ数学



三角比 内接円の半径の求め方をイチから丁寧にやってみよう 数スタ




高校数学 三角形の外接円の半径 内接円の半径と面積の関係 S 1 2r A B C 受験の月



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典



1




高校数学 内接円の半径の求め方 例題編 映像授業のtry It トライイット




円周の求め方と円の面積について アタリマエ



円の面積 直径 半径 円周の計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ




三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ



円の面積を 一般的に知られている公式を使わずに算出する方法を教えてくれませんか Quora




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ




正弦定理の公式 証明 使い方を徹底解説 例題あり 受験スタイル



内接円の半径



数学i Aチェック リピート 第4章 2図形への応用 4 外接円 内接円の半径 Pukiwiki
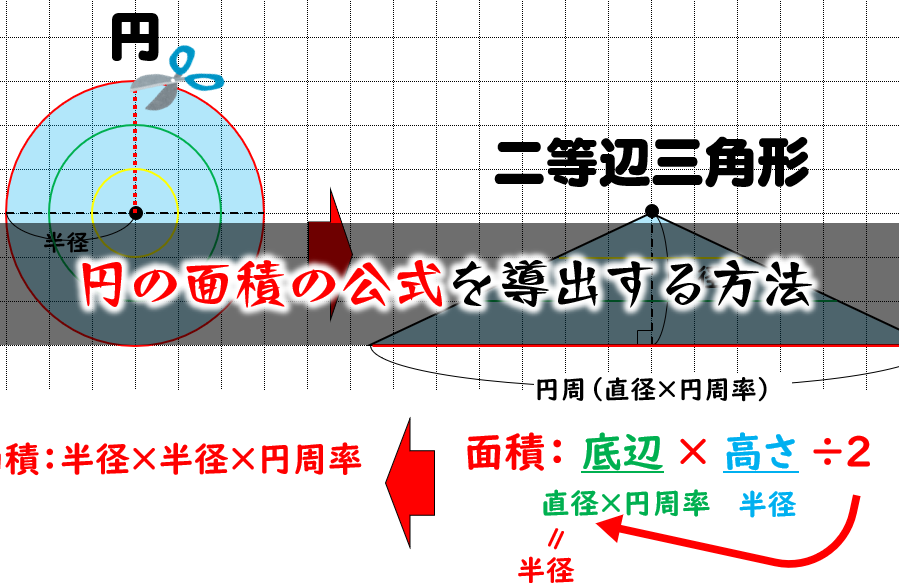



円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun




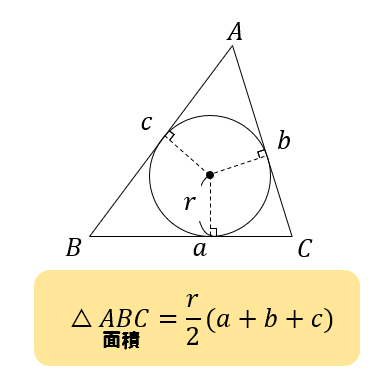
三角形の内接円 三角形の面積を求める公式の証明 数学i By ふぇるまー マナペディア




三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ
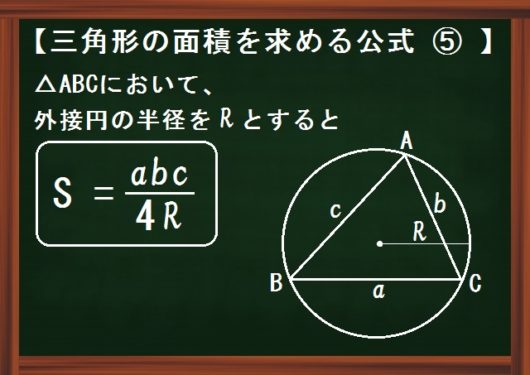



三角形の面積を求める公式7選 高校数学のまとめにどうぞ




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




四角形の外接円の半径の求め方 数学甲子園2014予選問題13の解説 テンメイのrun bike




高校数学 円に内接する四角形の計量 基本と裏技のまとめ トレミーの定理 ブラーマグプタの公式他 受験の月




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




公式を図解 すい体の体積 円すいの表面積の求め方




円の半径を求める 4つの方法 Wikihow



0 件のコメント:
コメントを投稿